Linear Convolution Sum Method

CONVOLUTION

LINEAR CONVOLUTION SUM METHOD

1.        This method is powerful analysis tool for studying LSI Systems.

2.        In this method we decompose input signal into sum of elementary signal. Now the elementary input signals are taken into account and individually given to the system. Now using linearity property whatever output response we get for decomposed input signal, we simply add it & this will provide us total response of the system to any given input signal.

3.        Convolution involves folding, shifting, multiplication and summation operations.

4.        If there are M number of samples in x(n) and N number of samples in h(n) then the maximum number of samples in y(n) is equals to M+n-1.

Linear Convolution states that

y(n) = x(n) * h(n)

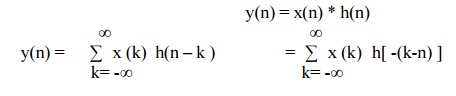
Example 1: h(n) = { 1 , 2 , 1, -1 } & x(n) = { 1, 2, 3, 1 } Find y(n)

METHOD 1: GRAPHICAL REPRESENTATION

Step 1) Find the value of n = nx+ nh = -1 (Starting Index of x(n)+ starting index of h(n))

Step 2) y(n)= { y(-1) , y(0) , y(1), y(2), ….} It goes up to length(xn)+ length(yn) -1. i.e n=-1

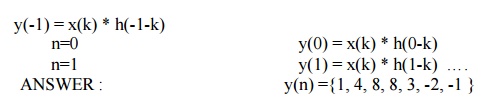
METHOD 2: MATHEMATICAL FORMULA

Use Convolution formula

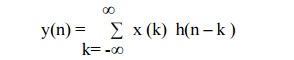
k= 0 to 3     (start index to end index of x(n))

y(n) = x(0) h(n) + x(1) h(n-1) + x(2) h(n-2) + x(3) h(n-3)

METHOD 3: VECTOR FORM (TABULATION METHOD)

X(n)= {x1,x2,x3} &       h(n) ={ h1,h2,h3}

y(-1) = h1 x1

y(0) = h2 x1 + h1 x2

y(1) = h1 x3 + h2x2 + h3 x1 …………

METHOD 4: SIMPLE MULTIPLICATION FORM