Relationship Between Fourier Transform and Z Transform

RELATIONSHIP BETWEEN FOURIER TRANSFORM AND Z TRANSFORM.

There is a close relationship between Z transform and Fourier transform. If we replace the complex variable z by e –jω, then z transform is reduced to Fourier transform.

Z transform of sequence x(n) is given by   

Fourier transform of sequence x(n) is given by

Complex variable z is expressed in polar form as Z= rejω where r= |z| and ω is ∟z. Thus we can be written as

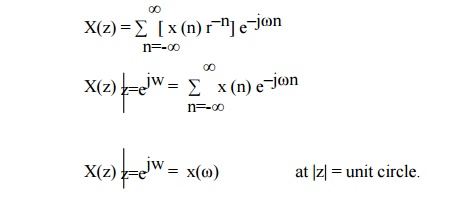
Thus, X(z) can be interpreted as Fourier Transform of signal sequence (x(n) r–n). Here r–n grows with n if r<1 and decays with n if r>1. X(z) converges for |r|= 1. hence Fourier transform may be viewed as Z transform of the sequence evaluated on unit circle. Thus The relationship between DFT and Z transform is given by

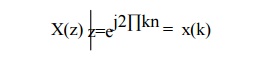
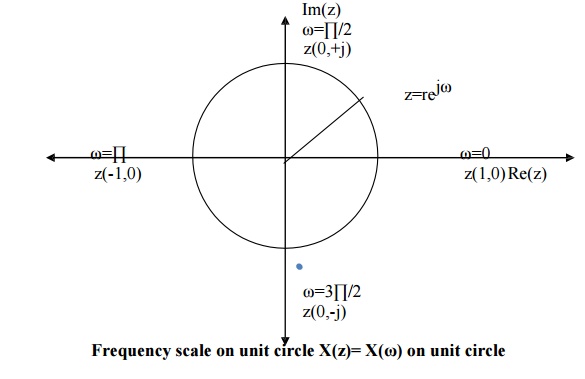
The frequency ω=0 is along the positive Re(z) axis and the frequency ∏/2 is along the positive Im(z) axis. Frequency ∏ is along the negative Re(z) axis and 3∏/2 is along the negative Im(z) axis.