Chapter: Digital Signal Processing : Signals and System
Properties of Z Transform (ZT)
PROPERTIES OF Z TRANSFORM (ZT)
1) Linearity
The linearity property states that if z
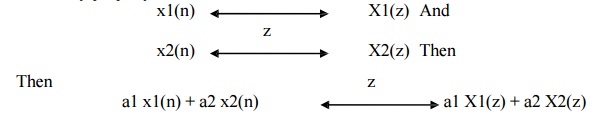
z Transform of linear combination of two or more signals is equal to the same linear combination of z transform of individual signals.
2) Time shifting
The Time shifting property states that if z x(n)

Thus shifting the sequence circularly by „k samples is equivalent to multiplying its z transform by z –k
3) Scaling in z domain
This property states that if

Thus scaling in z transform is equivalent to multiplying by an in time domain.
4) Time reversal Property
The Time reversal property states that if z

It means that if the sequence is folded it is equivalent to replacing z by z-1 in z domain.
5) Differentiation in z domain
The Differentiation property states that if z

6) Convolution Theorem
The Circular property states that if z
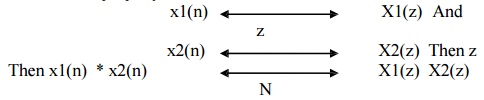
Convolution of two sequences in time domain corresponds to multiplication of its Z transform sequence in frequency domain.
7) Correlation Property
The Correlation of two sequences states that if z
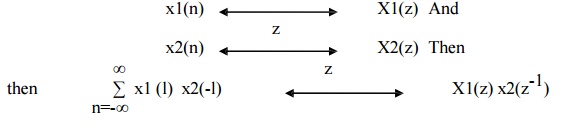
8) Initial value Theorem
Initial value theorem states that if z

9) Final value Theorem
Final value theorem states that if z

Related Topics