Properties of Linear Convolution

PROPERTIES OF LINEAR CONVOLUTION

x(n) = Excitation Input signal y(n)

= Output Response

h(n) = Unit sample response

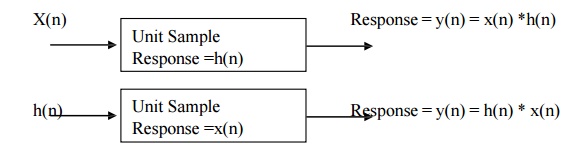
1. Commutative Law: (Commutative Property of Convolution)

x(n) * h(n) = h(n) * x(n)

2. Associate Law: (Associative Property of Convolution)

[ x(n) * h1(n) ] * h2(n) = x(n) * [ h1(n) * h2(n) ]

3. Distribute Law: (Distributive property of convolution) 

x(n) * [ h1(n) + h2(n) ] = x(n) * h1(n) + x(n) * h2(n)

CAUSALITY OF LSI SYSTEM

The output of causal system depends upon the present and past inputs. The output of the causal system at n= n0 depends only upon inputs x(n) for n≤ n0. The linear convolution is given as

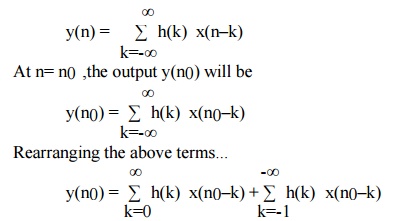
The output of causal system at n= n0 depends upon the inputs for n< n0 Hence h(-1)=h(-2)=h(-3)=0

Thus LSI system is causal if and only if

h(n) =0        for n<0

This is the necessary and sufficient condition for causality of the system. Linear convolution of the causal LSI system is given by

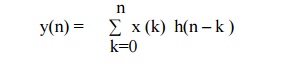
STABILITY FOR LSI SYSTEM

A System is said to be stable if every bounded input produces a bounded output.

The input x(n) is said to bounded if there exists some finite number Mx such that |x(n)| ≤ Mx < ∞. The output y(n) is said to bounded if there exists some finite number My such that |y(n)| ≤ My < ∞.

Linear convolution is given by

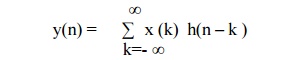
Taking the absolute value of both sides

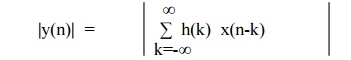
The absolute values of total sum is always less than or equal to sum of the absolute values of individually terms. Hence

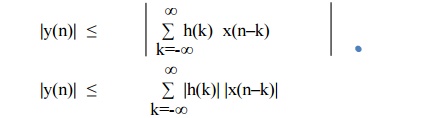
The input x(n) is said to bounded if there exists some finite number Mx such that |x(n)| ≤ Mx < ∞.

Hence bounded input x(n) produces bounded output y(n) in the LSI system only if

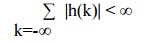
With this condition satisfied, the system will be stable. The above equation states that the LSI system is stable if its unit sample response is absolutely summable. This is necessary and sufficient condition for the stability of LSI system.

Example 1:

SELF-STUDY: Exercise No. 1

Q1) Show that the discrete time signal is periodic only if its frequency is expressed as the ratio of two integers.

Q2) Show that the frequency range for discrete time sinusoidal signal is -∏ to ∏ radians/sample or -½ cycles/sample to ½ cycles/sample.

Q3) Prove δ (n)= u(n)= u(n-1)

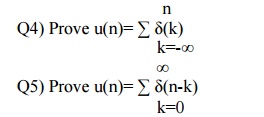
Q6) Prove that every discrete sinusoidal signal can be expressed in terms of weighted unit impulse. Q7) Prove the Linear Convolution theorem.