Discrete Time Signals and System

DISCRETE TIME SIGNALS AND SYSTEM

There are three ways to represent discrete time signals.

1) Functional Representation

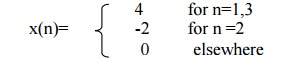
2) Tabular method of representation

3) Sequence Representation

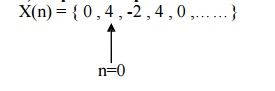
1. STANDARD SIGNAL SEQUENCES

1) Unit sample signal (Unit impulse signal)

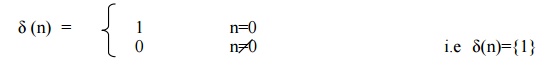
2) Unit step signal

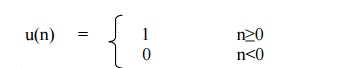
3) Unit ramp signal

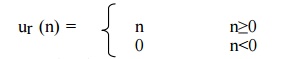
4) Exponential signal

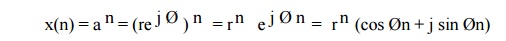
5) Sinusoidal waveform

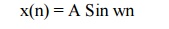
2. PROPERTIES OF DISCRETE TIME SIGNALS

1) Shifting : signal x(n) can be shifted in time. We can delay the sequence or advance the sequence. This is done by replacing integer n by n-k where k is integer. If k is positive signal is delayed in time by k samples (Arrow get shifted on left hand side) And if k is negative signal is advanced in time k samples (Arrow get shifted on right hand side)

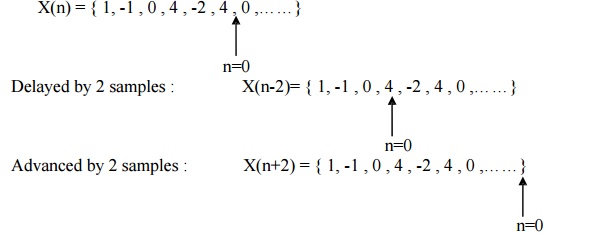
2) Folding / Reflection : It is folding of signal about time origin n=0. In this case replace n by – n.

3) Addition : Given signals are x1(n) and x2(n), which produces output y(n) where y(n) = x1(n)+ x2(n). Adder generates the output sequence which is the sum of input sequences.

4) Scaling: Amplitude scaling can be done by multiplying signal with some constant. Suppose original signal is x(n). Then output signal is A x(n)

4) Multiplication : The product of two signals is defined as y(n) = x1(n) * x2(n).

3. SYMBOLS USED IN DISCRETE TIME SYSTEM

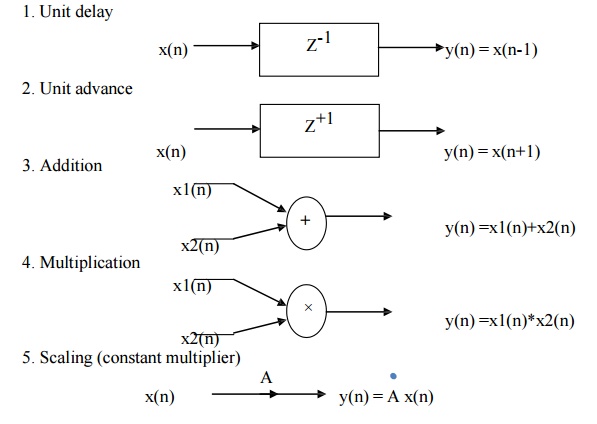
4. CLASSIFICATION OF DISCRETE TIME SYSTEMS

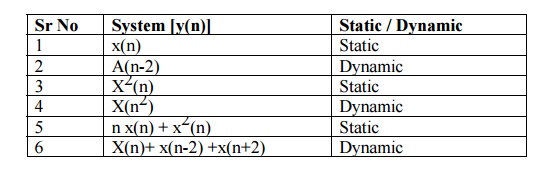
1. STATIC v/s DYNAMIC

It is very easy to find out that given system is static or dynamic. Just check that output of the system solely depends upon present input only, not dependent upon past or future.

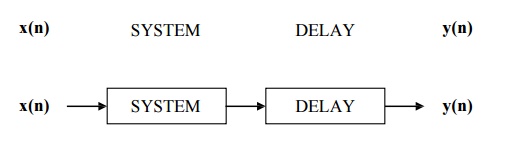
2) TIME INVARIANT v/s TIME VARIANT SYSTEMS

It is very easy to find out that given system is Shift Invariant or Shift Variant. Suppose if the system produces output y(n) by taking input x(n)                                    

                                                                             x(n)  -> y(n)                  

If we delay same input by k units x(n-k) and apply      it to same systems, the system produces output y(n-k)

                                                x(n-k) ->  y(n-k)            

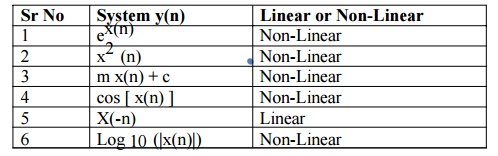
3) LINEAR v/s NON-LINEAR SYSTEMS

hence T [ a1 x1(n) + a2 x2(n) ] = T [ a1 x1(n) ] + T [ a2 x2(n) ] It is very easy to find out that given system is Linear or Non-Linear.

Response to the system to the sum of signal = sum of individual responses of the system.

4) CAUSAL v/s NON CAUSAL SYSTEMS

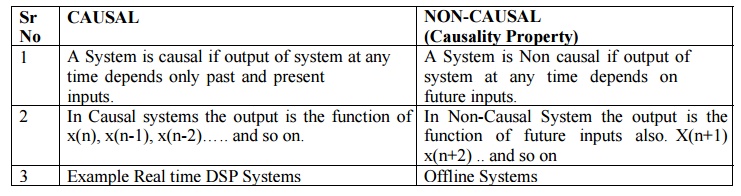
CAUSAL

a)        A System is causal if output of system at any time depends only past and present inputs.

b)       In Causal systems the output is the function of x(n), x(n-1), x(n-2)….. and so on.

c)        Example Real time DSP Systems

NON-CAUSAL (Causality Property)

a)        A System is Non causal if output of system at any time depends on future inputs.

b)       In Non-Causal System the output is the function of future inputs also. X(n+1) x(n+2) .. and so on

c)        Offline Systems

It is very easy to find out that given system is causal or non-causal. Just check that output of the system depends upon present or past inputs only, not dependent upon future.

Sr No          System [y(n)]       Causal /Non-Causal

1    x(n) + x(n-3)   Causal

2    X(n)      Causal

3    X(n) + x(n+3) Non-Causal

4    2 x(n)    Causal

5    X(2n)    Non-Causal

6    X(n)+ x(n-2) +x(n+2)        Non-Causal

5) STABLE v/s UNSTABLE SYSTEMS

STABLE

a)        A System is BIBO stable if every bounded input produces a bounded output.

b)       The input x(n) is said to bounded if there exists some finite number Mx such that |x(n)| ≤ Mx < ∞

The output y(n) is said to bounded if there exists some finite number My such that |y(n)| ≤ My < ∞

UNSTABLE (Stability Property)

a)        A System is unstable if any bounded input produces a unbounded output.

STABILITY FOR LTI SYSTEM

It is very easy to find out that given system is stable or unstable. Just check that by providing input signal check that output should not rise to ∞.

The condition for stability is given by

Sr No          System [y(n)]       Stable / Unstable

1    Cos [ x(n) ]     Stable

2    x(-n+2)           Stable

3    |x(n)|               Stable

4    x(n) u(n)                   Stable

5          X(n) + n x(n+1)       Unstable