Try these, Recap Exercise, Student Activities, Think and answer

Try these

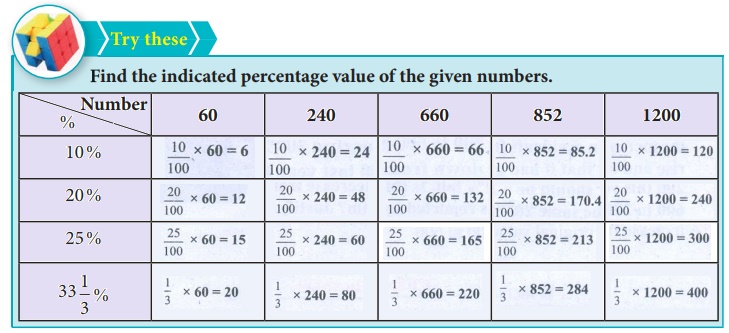
1. What percentage of a day is 10 hours?

Solution:

In a day, there are 24 hours

∴ 10 hrs out of 24 hrs is 10/24

As a percentage, we need to multiply by 100

∴  Percentage = [10/24] × 100 = 41.67%

2. Divide ₹350 among P, Q and R such that P gets 50% of what Q gets and Q gets 50% of what R gets.

Solution:

Let R get x, Q gets 50% of what R gets

        ∴  Q gets = (50/100) × x = x/2

P gets 50% of what Q gets

∴ P gets = 50/100 × x/2 = x/4

Since 350 is divided among the three

∴  350 = x + x/2 + x/4

350 = [4x + 2x + x ] / 4 = 7x / 4 = 350

 x = [350 × 4] / 7 = 200

Q gets = x/2 = 200/2 = 100, P gets = x/4 = 200/4 = 50

∴ P = 50, Q = 100, R = 200

Think

With a lot of pride, the traffic police commissioner of a city reported that the accidents had decreased by 200% in one year. He came up with this number by stating that the increase in accidents from 200 to 600 is clearly a 200% rise and now that it had gone down from 600 last year to 200 this year should be a 200% fall. Is this decrease from 600 to 200, the same 200% as reported by him? Justify.

Solution:

Increase from original value 200 to 600

% increase = [ Change in value / original value ] × 100

= [(600 – 200) / 600] × 100 = [400 / 200] × 100 = 200 % increase

Decrease from original value 600 to 200

% decrease = [ Change in value / original value ] × 100

here original value is 600

% decrease = [ (600 – 200) / 600 ] × 100 = [ 400 / 600 ] × 100 = 66.67 % increase

Increase from 200 → 600 and % decrease from 600 → 200 are not the same

Try these

• If the selling price of an article is less than the cost price of the article, then there is a ________.

Solution: Loss

• An article costing ₹5000 is sold for ₹4850. Is there a profit or loss? What percentage is it?

Solution: Loss

Percentage of Loss = [ (C.P – S.P) / C.P ] × 100

= [(5000 – 4850) / 5000] × 100

= [150 / 5000] × 100 = 3%

• If the ratio of cost price and the selling price of an article is 5:7, then the profit/ gain is_________%.

Solution:

C.P  = 5x

S.P = 7x

Profit = 7x – 5x = 2x

Profit Percentage = 7x – 5x = [ 2x / 5x ] × 100 = 40%

Think

A shopkeeper marks the price of a marker board 15% above the cost price and then allows a discount of 15% on the marked price. Does he gain or lose in the transaction?

Solution:

Let cost price of marker board be 100

CP = 100 Marks it 15% above CP

∴  Marked price = MP = ( [15/100] × CP ) + CP

= ( [15/100] × 100 ) + 100 = 15 + 100 = 115

Discount % = 15%

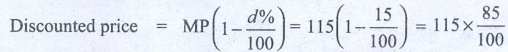
Discounted price = MP (1 – (d%/100)) = 115 (1 – (15/100)) = 115 × (85/100) = 97.75

∴ He sells it 97.75 which is less than his cost price. Therefore he loses

Loss = 97.75 − 100 = −2.25

Try these

1. The formula to find the simple interest for a given principal is __________.

Solution: PNR / 100

2. Find the simple interest on ₹900 for 73 days at 8 % p.a.

Solution:

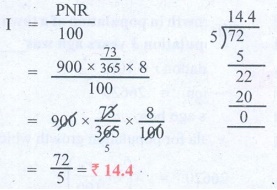
Solution 2:

I = PNR / 100

= [ 900 × (73/365) × 8 ] / 100

= 900 × (73/365) × (8 / 100)

= 72/5 = ₹ 14.4.

3. In how many years will ₹2000 become ₹3600 at 10 % p.a simple interest?

Solution:

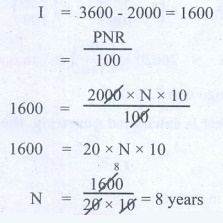
Solution 2:

I = 3600 – 2000 = 1600

= PNR / 100

1600 = [ 2000 × N × 10] / 100

1600 = 20 × N × 10

N = 1600 / [20 × 10] = 8years

Try these

1. Classify the given examples as direct or inverse proportion:

(i) Weight of pulses to their cost.

Answer: 

As weight increases cost also increases.

∴ Weight and cost are direct proportion.

(ii) Distance travelled by bus to the price of ticket.

Answer:

As the distance increases price to travel also increases.

∴ Distance and price are direct proportion.

(iii) Speed of the athelete to cover a certain distance.

Answer:

As the speed increases, the time to cover the distance become less.

So speed and time are in indirect proportion.

(iv) Number of workers employed to complete a construction in a specified time.

Answer:

As the number of workers increases, the amount of work become less, so they are in indirect proportion.

(v) Area of a circle to its radius.

Answer:

If the radius of the circle increases its area also increases.

∴  Area and radius of circles are direct proportion.

2. A student can type 21 pages in 15 minutes. At the same rate, how long will it take the student to type 84 pages?

Solution:

Direct proportion

No. of minutes = x 

k = 21/15

21/15 = 84/x

x = [84 × 15] / 21 = 60

3. If 35 women can do a piece of work in 16 days, in how many days will 28 women do the same work?

Solution:

Inverse proportion

No. of days = x

k = 35 × 16

∴  28 × x =  35 × 16

x = [ 35 × 16 ] / 28 = 20 days

Try these

1. If x and y vary directly, find k when x = y = 5 .

Solution:

If x and y vary directly then x/y = k.

Here x = 5 ; y = 5

∴ k = 5/5

k = 1

2. If x and y vary inversely, find the constant of proportionality when x = 64 and y = 0.75

Solution:

Given x = 64, y = 0.75 and also given x and y vary inversely.

∴ xy = k. the constant of variation.

∴ Constant = 64 × 0.75

Constant of variation = 48

Activity

Draw a circle of a given radius. Then, draw its radii in such a way that the angles between any two consecutive pair of radii are equal. Start drawing 3 radii and end with drawing 12 radii in the circle. List and prepare a table for the number of radii to the angle between a pair of consecutive radii and check whether they are in inverse proportion. What is the proportionality constant?

Solution:

As the number of radii increases angle decreases.

Hence they are in inverse proportion

∴ xy = 4 proportional constant

3 × 120° = 360° = k = 360°

Try these

Identify the different variations present in the following questions:

1. 24 men can make 48 articles in 12 days. Then, 6 men can make _____ articles in 6 days.

Solution:

Let the required no. of articles be x

(i) Mens and days are Indirect variables.

(ii) Men and Articles are direct variables

(iii) Days and articles are also direct variables using formula.

Let P1 = 24 D1 = 12  W1 = 48

P2 = 6  D2 = 6 W2 = x

[ P1 × D1 ] / W1 = [P2 × D2] / W2

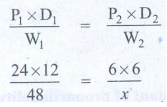
[24 × 12] / 48 = [6 × 6] / x

x = [ 6 × 6 × 48] / [24 × 12]

x =  6 Articles

2. 15 workers can lay a road of length 4 km in 4 hours. Then, _____ workers can lay a road of length 8 km in 8 hours.

Solution:

Let the required number of workers be x

(i) Length and workers are direct variable as more length need more workers.

The proportion is 4 : 8 : : 15 : x ………..(1)

(ii) Hours and workers are indirect variables as more working hours need less men.

∴ The proportion is 8 : 4 : : 15 : x ……..(2)

Combining (1) and (2)

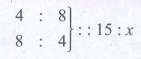
Product of the extremes = Product of the means

4 × 8 × x = 8 × 4 × 15

x = [ 8 × 4 × 15 ] / [ 4 × 8 ]

x = 15 workers

3. 25 women working 12 hours a day can complete a work in 36 days. Then, 20 women must work _____ hours a day to complete the same work in 30 days.

Solution:

Let the required hours be x.

As women increases hours to work decreases

∴ It is an inverse proportion.

∴ Multiplying factor is 25/20

As days increases hours needed become less

∴ It is also an indirect variation.

∴ Multiplying factor is 36/30

∴ x = 12 × [25/20] × [36/30]

x = 18 hours

4. In a camp there are 420 kg of rice sufficient for 98 persons for 45 days. The number of days that 60 kg of rice will last for 42 persons is _____.

Solution:

Let the required number of days be x.

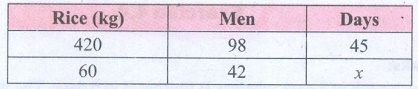
If amount of rice is more it will last for more days.

∴ It is Direct Proportion

∴ Multiplying factor is 60 / 420

If men increases number of days the rice lasts decreases

∴ It is an inverse proportion.

∴ Multiplying factor is 98 / 42

x = 45 × [60/420] × [98/42]

x = 15 days

Try these

1. Vikram can do one-third of a work in p days. He can do 3/4 th of the same work in _______ days.

Solution:

1/3 of the work will be done in p days.

∴ Full work will be completed in 3 p days

3/4 th of the work will be done in = 3p × 3/4

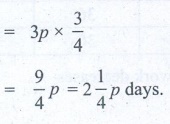
 = 2 (1/4) p days.

2. If m persons can complete a work in n days, then 4m persons can complete the work in _______days and m/4 persons can complete the same work in _______ days.

Solution:

Given m persons complete a work in n days

(i) Then work measured in terms of Man days = mn

4 m men do the work it will be completed in mn/4m days = n/4 days.

(ii) m/4 persons can complete the same work in (mn) / (m/4) days = (4mn) / (m) = 4n days

Note

For any given number, when it is increased first by x % and then decreased by y %, then the value of the number is increased or decreased by ( x + y + [xy/100] )% . Use ‘negative’ sign for decrease and also assume ‘decrease’ if the sign is negative. Use this note to check the answer for the Example 4.5.

Note

• If there are 2 successive discounts of a % and b % respectively, then

• Single discount in % equivalent to 3 successive discounts of a %, b % and c % respectively =

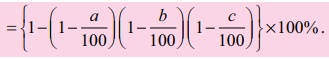
(Use this formula for the Example 4.11 and check the answer).

Note

There are situations where neither direct proportion nor indirect proportion can be applied. For example, if one can see a parrot at a distance through one eye, it does not mean that he can see two parrots at the same distance through both the eyes. Also, if it takes 5 minutes to fry a vadai, it does not mean that it will take 100 minutes to fry 20 vadais!

Note

The time taken to complete a work or task depends on various factors such as number of persons, their capacity to do the work, the amount of work and the time spent per day for the completion of work.

Note

If A is a/b times as good a worker as B, then A will only b/a of the time taken by B to complete the work. Try to solve the above Example 4.25 using this.