Time and Work

Time and Work

How would you find the answer for the following question?

If Kani can finish a given work in 2 hours and Viji in 3 hours, then in what time can they finish it working together? The answer for this question will be known here in this section.

Work to be done is usually considered as one unit. Work can be in any form like building a wall, making a road, filling or emptying a tank or even eating a certain amount of food.

Time is measured in hours, days etc., Certain assumptions are made that the work so done is uniform and each person shares the same work time in case of group work in completing the work.

Unitary Method

If two persons X and Y can complete some work individually in a and b days, then their one day’s work will be 1/a and 1/b respectively.

Working together, their one day’s work = 1/a + 1/b = a+b / ab  and so,

X and Y together can complete the work in   days.

Example 4.23

A and B together can do a piece of work in 16 days and A alone can do it in 48 days. How long will B take to complete the work?

Solution:

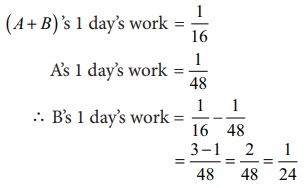
B alone can complete the work in 24 days.

Note

The time taken to complete a work or task depends on various factors such as number of persons, their capacity to do the work, the amount of work and the time spent per day for the completion of work.

Example 4.24

P and Q can do a piece of work in 20 days and 30 days respectively. They started the work together and Q left after some days of work and P finished the remaining work in 5 days. After how many days from the start did Q leave?

Solution:

Solution 2:

P’s 1 day’s work = 1/20 and Q’s 1 day’s work = 1/30

P’s work for 5 days = 1/20 × 5 = 5/20 = 1/4

Therefore, the remaining work = 1− 1/4 = 3/4 (as the total work is always 1). This remaining work was done by both P and Q.

Work done by P and Q in a day = 1/20 + 1/30 = 5/60 = 1/12

Therefore, the number of days they worked together = (3/4) / (1/12) = 3/4 × 12/1  = 9 days.

So, Q left after 9 days from the day the work started.

Example 4.25

A works 3 times as fast as B and is able to complete a work in 24 days less than the days taken by B. Find the time in which they can complete the work together.

Solution:

If B does the work in 3 days, then A will do it in 1 day. That is, the difference is 2 days. Here, given that the difference between A and B in completing the work is 24 days. Therefore, A will take 24/2 = 12 days and B will take 3 × 12 = 36 days to complete the work separately.

Hence, the time taken by A and B together to complete the work = days .

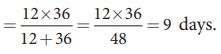
Note

If A is a/b times as good a worker as B, then A will only b/a of the time taken by B to complete the work. Try to solve the above Example 4.25 using this.

1. Sharing of the money for work

When a group of people do some work together, based on their individual work they get a share of money themselves. In general, money earned is shared by people, who worked together, in the ratio of the total work done by each of them.

• If the ratio of the time taken by A and B in doing a work is x : y, then the ratio of work done by A and B is 1/x : 1/y = y : x . This is the ratio for their separate wages too.

• If three persons A, B and C can do a work in x, y and z days respectively, then the ratio in which their wages will be distributed to them is 1/x : 1/y : 1/z .

Example 4.26

X, Y and Z can do a piece of job in 4, 6 and 10 days respectively. If X,Y and Z work together to complete, then find their separate shares if they will be paid ₹ 31000 for completing the job.

Solution:

Since they all work together for the same number of days (60/31) , the ratio in which they share the money is equal to the ratio of their work done per day.

That is, it is equal to  

1/4 : 1/6 : 1/10 = 15/60 : 10/60 : 6/60 =15:10:6

Here, the total parts = 15 + 10 + 6 = 31

Hence, A’ s share = (15/31) × 31000 = ₹15000 , B’ s share = (10/31) × 31000 = ₹10000 and C’ s share is ₹31000 − (₹15000 + ₹10000)= ₹6000.

Try these

1. Vikram can do one-third of a work in p days. He can do 3/4 th of the same work in _______ days.

Solution:

1/3 of the work will be done in p days.

∴ Full work will be completed in 3 p days

3/4 th of the work will be done in = 3p × 3/4

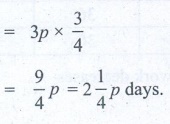
 = 2 (1/4) p days.

2. If m persons can complete a work in n days, then 4m persons can complete the work in _______days and m/4 persons can complete the same work in _______ days.

Solution:

Given m persons complete a work in n days

(i) Then work measured in terms of Man days = mn

4 m men do the work it will be completed in mn/4m days = n/4 days.

(ii) m/4 persons can complete the same work in (mn) / (m/4) days = (4mn) / (m) = 4n days