Compound Variation

Compound Variation

Before we could learn about compound variation, let us recall the concepts on direct and inverse proportions.

If two quantities are such that an increase or decrease in one quantity makes a corresponding increase or decrease (same effect) in the other quantity, then they are said to be in direct proportion or said to vary directly. In other words, x and y are said to vary directly if y=kx always, where k is called the proportionality constant and k > 0 assuming that y depends on x and so k = y/x.

For example, let us assume that one of you plan to give 2 pens to each of your friends in the birthday party. Then the number of pens to be bought will be in direct proportion with the number of friends who will attend the party. Isn’t it? The following table will help you understand this clearly.

In this case, we find that the proportionality constant, k = y/x = 2/1 = 4/2 = 10/5 = 24/12 = 30/15 = 2 .

Few more examples of Direct Proportion:

1. Distance –Time (under constant speed): If the distance increases, then the time taken to reach that distance will also increase and vice- versa.

2. Purchase – Spending: If the purchase on utilities for a family during the festival time increases, then the spending limit also increases and vice versa.

3. WorkTime – Earnings: If the number of hours worked is less, then the pay earned will also be less and vice-versa.

Similarly, if two quantities are such that an increase or decrease in one quantity makes a corresponding decrease or increase (opposite effect) in the other quantity, then they are said to be in inverse (indirect) proportion or said to vary inversely. In other words, x and y are said to vary inversely, if xy = k always, where k is called proportionality constant and k > 0.

For example, let us assume that a class of 30 students in a school walks on streets in a village for health awareness campaign in an orderly manner, then we can see an inverse proportion in the number of rows and columns they walk. The following table will help you understand this clearly.

We can map a few of these arrangements as  (5 rows/6 columns)and  (6 rows/5 columns) and see the opposite variations in rows and columns.

In this case, we find that the proportionality constant, k is 30.

Few more examples of Inverse Proportion:

1. Price – Consumption: If the price of consumable products increases, then naturally its consumption will decrease and vice-versa.

2. Workers – Time: If more workers are employed to complete a work, then the time taken to complete the work will be less and vice-versa.

3. Speed – Time (Fixed Distance): If we travel with less speed, then the time taken to cover a given distance will be more and vice-versa.

Now, use the concept of direct and inverse proportions and try to answer the following questions:

Try these

1. Classify the given examples as direct or inverse proportion:

(i) Weight of pulses to their cost.

Answer: 

As weight increases cost also increases.

∴ Weight and cost are direct proportion.

(ii) Distance travelled by bus to the price of ticket.

Answer:

As the distance increases price to travel also increases.

∴ Distance and price are direct proportion.

(iii) Speed of the athelete to cover a certain distance.

Answer:

As the speed increases, the time to cover the distance become less.

So speed and time are in indirect proportion.

(iv) Number of workers employed to complete a construction in a specified time.

Answer:

As the number of workers increases, the amount of work become less, so they are in indirect proportion.

(v) Area of a circle to its radius.

Answer:

If the radius of the circle increases its area also increases.

∴  Area and radius of circles are direct proportion.

2. A student can type 21 pages in 15 minutes. At the same rate, how long will it take the student to type 84 pages?

Solution:

Direct proportion

No. of minutes = x 

k = 21/15

21/15 = 84/x

x = [84 × 15] / 21 = 60

3. If 35 women can do a piece of work in 16 days, in how many days will 28 women do the same work?

Solution:

Inverse proportion

No. of days = x

k = 35 × 16

∴  28 × x =  35 × 16

x = [ 35 × 16 ] / 28 = 20 days

Let us now see what a Compound Variation is? There will be problems which may involve a chain of two or more variations in them. This is called as Compound Variation.

The different possibilities of two variations are:

Direct-Direct,

Direct-Inverse,

Inverse-Direct,

Inverse-Inverse.

Note

There are situations where neither direct proportion nor indirect proportion can be applied. For example, if one can see a parrot at a distance through one eye, it does not mean that he can see two parrots at the same distance through both the eyes. Also, if it takes 5 minutes to fry a vadai, it does not mean that it will take 100 minutes to fry 20 vadais!

Let us now solve a few problems on compound variation. Here, we compare the known quantity with the unknown (x). There are a few methods in practice by which problems on compound variation are solved. They are given as follows:

1. Proportion Method

In this method, we shall compare the given data and find whether they are in direct or inverse proportion. By finding the proportion, we can use the fact that

the product of the extremes = the product of the means

and get the value of the unknown (x).

2. Multiplicative Factor Method

Illustration:

Here, the unknown (x) is in men and so it is compared to the known, namely hours and days. If men and hours are in direct proportion (D), then take the multiplying factor as d/c (take the reciprocal). Also, if men and days are in inverse proportion ( I ), then take the multiplying factor as e/f (no change). Thus, we can find the unknown (x) in men as x = a × d/c × e/f.

3. Formula Method

Identify the data from the given statement as Persons (P), Days (D), Hours (H) and Work (W) and use the formula,

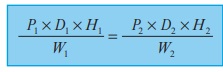
where the suffix 1 contains the complete data from the first statement of the given problem and the suffix 2 contains the unknown data to be found out in the second statement of the problem. That is, this formula says, P₁ men doing W₁ units of work in D₁ days working H₁ hours per day is the same as P₂ men doing W₂ units of work in D₂ days working H₂ hours per day. Identifying the work W₁ and W₂ correctly is more important in these problems. This method will be easy for finding the unknown (x) quickly.

Example 4.19

(Direct – Direct Variation)

If a company pays ₹6 lakh for 15 workers for 20 days, how much would it need to pay for 5 workers for 12 days?

Solution:

Proportion Method

Here, the unknown is the pay (x). It is to be compared with the workers and the days.

Step 1:

Here, less days means less pay. So, it is in direct proportion.

∴ The proportion is 20 : 12 :: 6 : x    ………1

Step 2:

Also, less workers means less pay. So, it is in direct proportion again.

∴ The proportion is 15 : 5 :: 6 : x  ………2

Step 3:

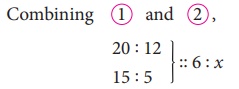
We know that, the product of the extremes = the product of the means

So, 20 ×15 × x = 12 ×6 × 5 ⇒ x = 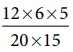 = (12×6×5) / (20×15) = ₹ 1.2 lakh.

Multiplicative Factor Method

Here, the unknown is the pay (x). It is to be compared with the workers and the days.

Step 1:

Here, less days means less pay. So, it is in direct proportion.

The multiplying factor is 12/20 (take the reciprocal).

Step 2:

Also, less workers means less pay. So, it is in direct proportion again.

The multiplying factor is 5/15 (take the reciprocal).

Step 3:

∴ x = 6 × 12/20 × 5/15 = ₹ 1.2 lakh.

Formula Method

Here, P₁ = 15, D₁ = 20 and W₁ = 6 . Also, P₂ =5, D₂ = 12 and W₂ = x

Using the formula, [P₁×D₁] / W₁= [P₂×D₂] / W₂

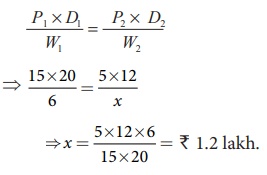
Example 4.20

(Direct – Inverse Variation)

A mat of length 180 m is made by 15 women in 12 days. How long will it take for 32 women to make a mat of length 512 m?

Solution:

Proportion Method

Here, the unknown is the days (x). It is to be compared with the length and the women.

Step 1:

Here, more length means more days. So, it is in direct proportion.

∴ The proportion is 180 : 512 :: 12 : x     ……………1

Step 2:

Also, more women means less days. So, it is in inverse proportion.

∴ The proportion is 32 : 15 :: 12 : x   ……………2

Step 3:

We know that, the product of the extremes = the product of the means

So, 180× 32 ×x = 512×12×15 ⇒ x = (512×12 ×15) /(180×32) =16 days.

Multiplicative Factor Method

Here, the unknown is the days (x). It is to be compared with the length and the women.

Step 1:

Here, more length means more days. So, it is in direct proportion.

The multiplying factor is 512/180 (take the reciprocal).

Step 2:

Also, more women means less days. So, it is in inverse proportion.

 The multiplying factor is 15/32 (no change).

Step 3:

∴ x = 12 × 512/180 × 15/32 = 16 days.

Formula Method:

Here, P₁ = 15, D₁ = 12 and W₁ = 180 and P₂ = 32, D₂ = x and W₂ = 512

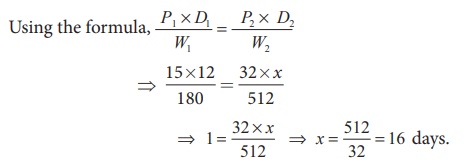
Remark: Students may answer in any of the three given methods dealt here.

Try these

1. If x and y vary directly, find k when x = y = 5 .

Solution:

If x and y vary directly then x/y = k.

Here x = 5 ; y = 5

∴ k = 5/5

k = 1

2. If x and y vary inversely, find the constant of proportionality when x = 64 and y = 0.75

Solution:

Given x = 64, y = 0.75 and also given x and y vary inversely.

∴ xy = k. the constant of variation.

∴ Constant = 64 × 0.75

Constant of variation = 48

Activity

Draw a circle of a given radius. Then, draw its radii in such a way that the angles between any two consecutive pair of radii are equal. Start drawing 3 radii and end with drawing 12 radii in the circle. List and prepare a table for the number of radii to the angle between a pair of consecutive radii and check whether they are in inverse proportion. What is the proportionality constant?

Solution:

As the number of radii increases angle decreases.

Hence they are in inverse proportion

∴ xy = 4 proportional constant

3 × 120° = 360° = k = 360°

Example 4.21 (Inverse – Direct Variation)

If 81 students can do a painting on a wall of length 448 m in 56 days, then how many students can do the painting on a similar type of wall of length 160 m in 27 days?

Solution:

Multiplicative Factor Method

Here, the unknown is the students (x). It is to be compared with the days and the length of the wall.

Step 1:

Here, less days means more students. So, it is in inverse proportion.

 The multiplying factor is 56/27 .

Step 2:

Also, less length means less students. So, it is in direct proportion.

 The multiplying factor is 160/448.

Step 3:

∴ x = 81× (56/27) × (160/448)

 x = 60 students.

Formula Method

Here, P₁ = 81, D₁ = 56 and W₁ = 448 and P₂ = x, D₂ = 27 and W₂ =160

Using the formula, P₁×D₁ /W₁ = P₂× D₂ /W₂

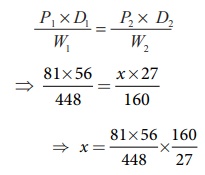
⇒ x = [(81×56)/448] × [160/27]

⇒ x = 60 students.

Example 4.22 (Inverse – Inverse Variation)

If 48 men working 7 hours a day can do a work in 24 days, then in how many days will 28 men working 8 hours a day can complete the same work?

Solution:

Multiplicative Factor Method

Here, the unknown is the days (x). It is to be compared with the men and the hours.

Step 1:

Here, less men means more days. So, it is in inverse proportion.

 The multiplying factor is 48/28.

Step 2:

Also, more hours means less days. So, it is in inverse proportion again.

 The multiplying factor is 7/8.

Step 3:

∴ x = 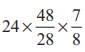 = 24 × (48/28) × (7/8) = 36 days.

Formula Method

Here, P₁ = 48, D₁ = 24, H₁ = 7 and W₁ = 1 (Why?)

P₂ = 28, D₂ = x , H₂ = 8 and W₂ = 1 (Why?)

Using the formula,

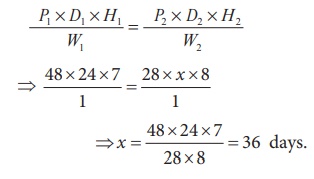
Try these

Identify the different variations present in the following questions:

1. 24 men can make 48 articles in 12 days. Then, 6 men can make _____ articles in 6 days.

Solution:

Let the required no. of articles be x

(i) Mens and days are Indirect variables.

(ii) Men and Articles are direct variables

(iii) Days and articles are also direct variables using formula.

Let P₁ = 24 D₁ = 12  W₁ = 48

P₂ = 6  D₂ = 6 W₂ = x

[ P₁ × D₁ ] / W₁ = [P₂ × D₂] / W₂

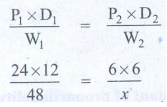
[24 × 12] / 48 = [6 × 6] / x

x = [ 6 × 6 × 48] / [24 × 12]

x =  6 Articles

2. 15 workers can lay a road of length 4 km in 4 hours. Then, _____ workers can lay a road of length 8 km in 8 hours.

Solution:

Let the required number of workers be x

(i) Length and workers are direct variable as more length need more workers.

The proportion is 4 : 8 : : 15 : x ………..(1)

(ii) Hours and workers are indirect variables as more working hours need less men.

∴ The proportion is 8 : 4 : : 15 : x ……..(2)

Combining (1) and (2)

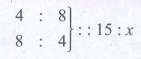
Product of the extremes = Product of the means

4 × 8 × x = 8 × 4 × 15

x = [ 8 × 4 × 15 ] / [ 4 × 8 ]

x = 15 workers

3. 25 women working 12 hours a day can complete a work in 36 days. Then, 20 women must work _____ hours a day to complete the same work in 30 days.

Solution:

Let the required hours be x.

As women increases hours to work decreases

∴ It is an inverse proportion.

∴ Multiplying factor is 25/20

As days increases hours needed become less

∴ It is also an indirect variation.

∴ Multiplying factor is 36/30

∴ x = 12 × [25/20] × [36/30]

x = 18 hours

4. In a camp there are 420 kg of rice sufficient for 98 persons for 45 days. The number of days that 60 kg of rice will last for 42 persons is _____.

Solution:

Let the required number of days be x.

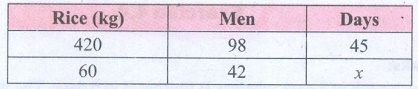
If amount of rice is more it will last for more days.

∴ It is Direct Proportion

∴ Multiplying factor is 60 / 420

If men increases number of days the rice lasts decreases

∴ It is an inverse proportion.

∴ Multiplying factor is 98 / 42

x = 45 × [60/420] × [98/42]

x = 15 days