Applications of Percentage in Word Problems

Applications of Percentage in Word Problems

We know that Per Cent means per hundred or out of a hundred. It is denoted by the symbol %_. x% denotes the fraction x/100. It is very useful in comparing quantities easily. Let us see its uses in the following word problems.

Example 4.1

If x % of 600 is 450, then find the value of x.

Solution:

Given, x % of 600 = 450

(x/100) × 600 = 450

x = 450/6

x = 75

Example 4.2

When a number is decreased by 25 % , it becomes 120. Find the number.

Solution:

Let the number be x .

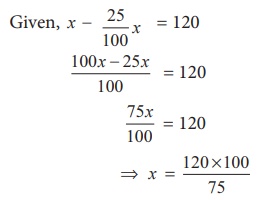
⇒ x = 160

Aliter: Using the above formula,

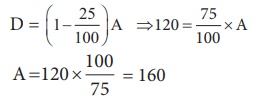
If we start with a quantity A and then decrease that quantity by x% , we will get the decreased quantity as,

 D = (1 − x/100) A

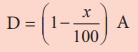
Example 4.3

Akila scored 80 % of marks in an examination. If her score was 576 marks, then find the maximum marks of the examination.

Solution:

Let the maximum marks be x .

Now, 80 % of x = 576

80/100 × x = 576

⇒ x = 576 × (100/80) = 720 marks

Therefore, the maximum marks of the examination = 720.

Example 4.4

If the price of Orid dhall after 20% increase is ₹96 per kg, then find the original price of Orid dhall per kg.

Solution:

Let the original price of Orid dhall be ₹ x .

New price after 20% increase

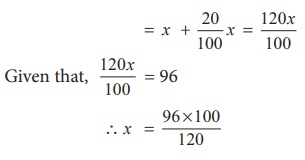
Aliter: Using the above formula,

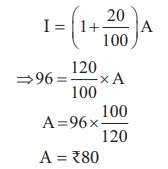
A=₹80

 If we start with a quantity A and then increase that quantity by x% , we will get the increased quantity as,

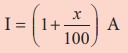
D = (1 + x/100) A

Try these

1. What percentage of a day is 10 hours?

Solution:

In a day, there are 24 hours

∴ 10 hrs out of 24 hrs is 10/24

As a percentage, we need to multiply by 100

∴  Percentage = [10/24] × 100 = 41.67%

2. Divide ₹350 among P, Q and R such that P gets 50% of what Q gets and Q gets 50% of what R gets.

Solution:

Let R get x, Q gets 50% of what R gets

        ∴  Q gets = (50/100) × x = x/2

P gets 50% of what Q gets

∴ P gets = 50/100 × x/2 = x/4

Since 350 is divided among the three

∴  350 = x + x/2 + x/4

350 = [4x + 2x + x ] / 4 = 7x / 4 = 350

 x = [350 × 4] / 7 = 200

Q gets = x/2 = 200/2 = 100, P gets = x/4 = 200/4 = 50

∴ P = 50, Q = 100, R = 200

Think

With a lot of pride, the traffic police commissioner of a city reported that the accidents had decreased by 200% in one year. He came up with this number by stating that the increase in accidents from 200 to 600 is clearly a 200% rise and now that it had gone down from 600 last year to 200 this year should be a 200% fall. Is this decrease from 600 to 200, the same 200% as reported by him? Justify.

Solution:

Increase from original value 200 to 600

% increase = [ Change in value / original value ] × 100

= [(600 – 200) / 600] × 100 = [400 / 200] × 100 = 200 % increase

Decrease from original value 600 to 200

% decrease = [ Change in value / original value ] × 100

here original value is 600

% decrease = [ (600 – 200) / 600 ] × 100 = [ 400 / 600 ] × 100 = 66.67 % increase

Increase from 200 → 600 and % decrease from 600 → 200 are not the same

Example 4.5

The income of a person is increased by 10% and then decreased by 10 % . Find the chang in his income.

Solution:

Let his initial income be ₹ x .

Income after 10% increase is

That is, income of the person is reduced by 1%.

Aliter:

Let his income be ₹100

Income after 10% increase is

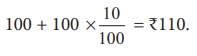
100 + 100 × (10/100) = ₹110.

Now, income after 10% decrease is,

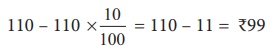
110 – 110 × (10/100) = 110–11= ₹99

∴ Net change in his income = 100 – 99 = 1

∴ Percentage change = 1/100 × 100% = 1% .

That is, income of the person is reduced by 1%.

Note

For any given number, when it is increased first by x % and then decreased by y %, then the value of the number is increased or decreased by ( x + y + [xy/100] )% . Use ‘negative’ sign for decrease and also assume ‘decrease’ if the sign is negative. Use this note to check the answer for the Example 4.5.