Compound Interest

Compound Interest

The most powerful force in this universe is _______. How would you complete this quote? The world renowned physicist Albert Einstein completed this quote with the word

Compound Interest.

When money is borrowed or deposited on simple interest ( ; I = PNR / 100 ), then the interest is calculated evenly on the principal throughout the loan or deposit period.

Try these

1. The formula to find the simple interest for a given principal is __________.

Solution: PNR / 100

2. Find the simple interest on ₹900 for 73 days at 8 % p.a.

Solution:

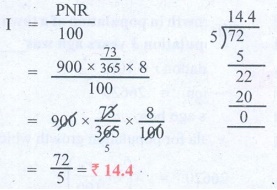
Solution 2:

I = PNR / 100

= [ 900 × (73/365) × 8 ] / 100

= 900 × (73/365) × (8 / 100)

= 72/5 = ₹ 14.4.

3. In how many years will ₹2000 become ₹3600 at 10 % p.a simple interest?

Solution:

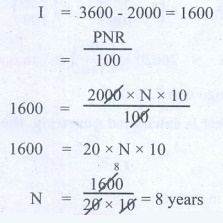
Solution 2:

I = 3600 – 2000 = 1600

= PNR / 100

1600 = [ 2000 × N × 10] / 100

1600 = 20 × N × 10

N = 1600 / [20 × 10] = 8years

In post offices, banks, insurance companies and other financial institutions, there is another type of interest calculation on offer. Here, the interest accrued during the first time period (say 6 months) is added to the original principal and the amount so obtained is taken as the principal for the second time period (that is, the next 6 months) and this keeps going on, up to the fixed time agreement between the banker and the depositer.

After a certain period, the difference between the amount and the money deposited is called the compound interest which is abbreviated as C.I. Clearly, the compound interest will be more than the simple interest just because the principal keeps on changing for every time period.

We call the time period after which the interest is added to the principal, as the conversion period. For example, if the interest is compounded say quarterly, there will be four conversion periods in a year, every 3 months. In such cases, the interest rate will be one fourth of the annual rate and the number of times that interest will be compounded is four times the number of years.

In case of simple interest, the principal remains the same for the whole duration where as in case of compound interest, the principal keeps on changing as per the conversion period. The simple interest and the compound interest remains the same for the first conversion period.

Illustration 1

To find the compound interest on ₹20000 for 4 years at 10 % p.a compounded annually and compare it with the simple interest obtained for the same.

Calculating Compound Interest

 ∴ Compound Interest for 4 years = A P = 29282 – 20000 = 9282

Calculating Simple Interest

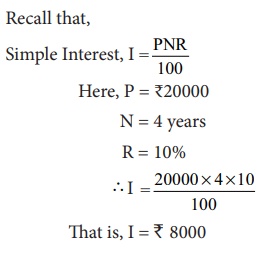
What we observe from the calculation of C.I is a repeated multiplication by the factor 1.1 as 20000 (×1.1 ), 22000 (×1.1 ), 24200 (×1.1 ), 26620 (×1.1 ) for 4 years.

We also note that the compound interest (₹9282) grows faster and is clearly more than the simple interest (₹8000) obtained. When the time period is longer, the above method is time consuming. So, to save time and to find the amount and the compound interest easily we have a formula as explained in the following illustration.

Illustration 2

To calculate the amount and compound interest for ₹1000 for 3 years at 10% p.a compound annually.

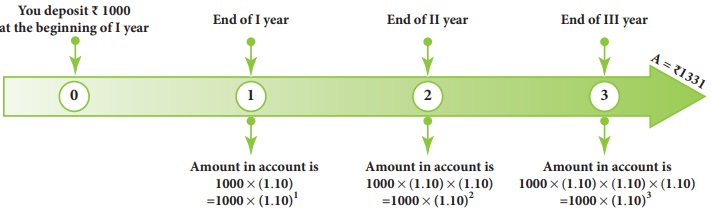
             Flow chart showing 10% interest being compounded annually

This leads to the pattern for Amount as P (1+ [r/100])for the I year, P(1+ [r/100]) (1+ [r/100]) for the II year, P (1+ [r/100]) (1+ [r/100]) (1+ [r/100]) for the III year and so on. In general, A=P (1+ [r/100])n for the nth year. Here, the amount after 3 years, A = 1000 (1+ [10/100])3 = ₹1331 and so, C.I = A − P = ₹331.

Do You Know: In 1626, Peter Minuit convinced the Wappinger Indians to sell him the Manhattan Island for 24 dollars. If the native Americans had put the 24 dollars into a bank account at 5 % interest rate compounded monthly, by the year 2020 there would be well over 5.5 billion (550 crores) dollars in the account! This is the might of compound interest!

The following formulae will be helpful in calculating the compound interest easily for the following time periods.

(i) When the interest is compounded annually, we have

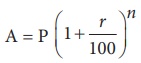
where A is the amount, P is the principal, r is the rate of interest per annum and n is the number of years and we shall get the compound interest as C.I = Amount – Principal.

(ii) When the interest is compounded half yearly, we have

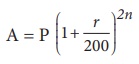
(iii) When the interest is compounded quarterly, we have

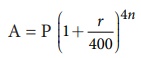
(iv) When the interest is compounded annually but rate of interest differs year by year, we have

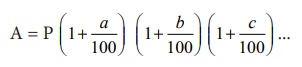
where a, b and c are interest rates for I, II and III years respectively.

(v) When interest is compounded annually but time period is in fraction say a (b/c) years, we have

(Use of calculators are permitted for lengthy calculations and also to verify answers).

Example 4.14

Find the C.I for the data given below:

(i) Principal = ₹4000, r = 5% p.a, n = 2 years, interest compounded annually.

(ii) Principal = ₹5000, r = 4% p.a, n = 1 1/2 years, interest compounded half-yearly.

(iii) Principal = ₹30000, r = 7% for I year, r = 8% for II year, compounded annually.

(iv) Principal = ₹10000, r = 8% p.a, n = 2 3/4 years, interest compounded yearly.

Solution:

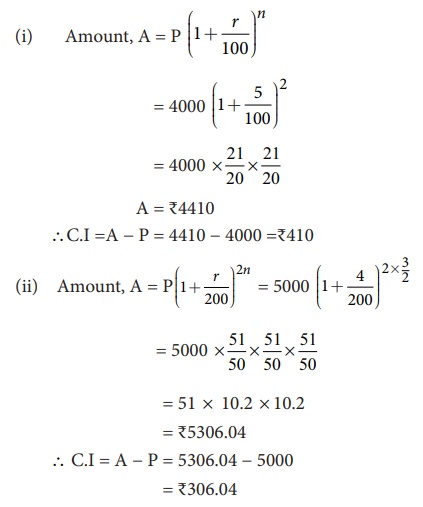
A = ₹12363.84

 C.I = A − P = 12363.84 − 10000 = ₹2363.84