Exercise 4.2 (Profit, Loss, Discount, Expenses and GST)

Exercise 4.2

1. Fill in the blanks:

(i) Loss or gain percentage is always calculated on the__________. [Answer: Cost price]

(ii) A mobile phone is sold for ₹8400 at a gain of 20%. The cost price of the mobile phone is________. [Answer: ₹ 7000]

Solution:

Let cost price of mobile be ₹ x

Given that selling price is ₹ 8400 and gain is 20%

As per formula,

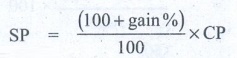
SP = [ (100 + gain %) / 100 ] × CP

∴  by substituting we get,

8400 = [ (100 + 20) / 100 ] × x

8400 = [120 / 100] x

 x = [8400 × 100] / 120 =  ₹ 7000

(iii) An article is sold for ₹555 at a loss of 7 1/2 %. The cost price of the article is ________. [Answer: ₹ 600 ]

Solution:

Given selling price is  ₹  555 & loss is 7 1/2%

as per formula,

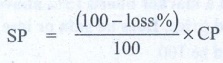
SP = [ (100−loss %) / 100 ] × CP

by substituting, we get

555 = [ (100 – 7 1/2) / 100 ] × CP

∴ 555 = [ (100 – 15/2) /100 ] × CP = [ ( (200 – 15)/2) / 100 ] × CP

555 = [ (185/2) / 100 ] × CP

∴  CP = (555 × 100) / (185/2) = [ (555 × 100) / 185 ] × 2 =  ₹ 600

(iv) A mixer grinder marked at ₹4500 is sold for ₹4140 after discount. The rate of discount is __________. [Answer: 8%]

Solution:

Marked price is ₹ 4500

Discounted price in ₹ 4140

∴ Discount = Marked price − Discounted price

= 4500 − 4140 = 360

∴  Rate of discount = [ Discount / Marked Price ] × 100

= [360 / 4500] × 100 = 8%

(v) The total bill amount of a shirt costing ₹575 and a T-shirt costing ₹325 with GST of 5% is_______. [Answer: ₹ 945]

Solution:

Cost price of shirt = ₹ 575 (CP)

GST = 5%

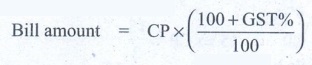
Bill amount formula = CP × [ (100 + GST%) / 100]

= 575 × [(100 + 5) / 100] = 575 × [105 / 100] = ₹ 603.75

Cost price of T−shirt = ₹ 325 (CP)

GST = 5%

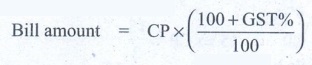
Bill amount = CP × [ (100 + GST%) / 100]

= 325 × [ (100 + 5) / 100 ] =  ₹ 341.25

∴ Total bill amount = ₹ 603.75 + ₹ 341.25 = ₹ 945

2. If selling an article for ₹820 causes 10% loss on the selling price, then find its cost price.

Solution 1:

Solution 2:

Given that selling price (SP) = ₹ 820

Loss % = 10%

As per formula SP = CP × [ (100 – loss%) / 100 ]

∴ Substituting in formula, we get

820 = CP × [ (100 – 10) / 100]

∴  CP =  [ 820 × 100 ] / 90 = 911

3. If the profit earned on selling an article for ₹810 is the same as loss on selling it for ₹530, then find the cost price of the article.

Solution:

Case 1: Profit = Selling price (SP) − Cost price (CP)

Case 2: Loss = Cost price (CP) − Selling price (SP)

Given that profit of case 1 = loss of case 2

∴  P = 810 − CP

L = CP − 530

Since profit (P) = loss (L)

810 − CP = CP − 530

∴  2CP = 810 + 530 = 1340 ⇒ C.P = 1340/2

∴   CP = 670

4. If the selling price of 10 rulers is the same as the cost price of 15 rulers, then find the profit percentage.

Solution:

Let cost price of one ruler be x

Given that selling price (SP) of 10 rulers,

i.e., same as cost price (CP) of 15 rulers

∴  SP of 10 rulers = 15 × x = 15x

∴ SP of 1 ruler = 15x / 10 = 1.5x

∴ Gain = SP of 1 ruler − CP of 1 ruler = 1.5x − x = 0.5x

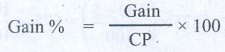
Gain % = [ Gain / CP ] × 100 = [ 0.5x / x ] × 100 = 50%

5. Some articles are bought at 2 for ₹15 and sold at 3 for ₹25. Find the gain percentage.

Solution:

Let cost price of one article be C.P

Given that 2 are bought for  ₹ 15

∴ 2 × CP = 15 ⇒ CP= 15/2

Let selling price of one article be SP

Given that 3 are sold for ₹ 25

∴ 3 × SP = 25 ⇒ SP = 25/3

∴ Gain = SP – CP = 25/3 – 15/2 = [50 – 45] / 6 = 5/6

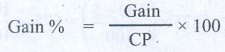
Gain % = [Gain / CP] × 100 = [ (5/6) / (15/2) ] × 100 = [ 5/6 × 2/15 ] × 100 = 100/9

= 11 1/9 %

6. By selling a speaker for ₹768, a man loses 20%. In order to gain 20%, how much should he sell the speaker?

Solution 1:

Solution 2:

Selling price (SP) of speaker = ₹ 768

Loss % = 20%

as per formula

SP = CP × [ (100 − loss %) / 100 ]

∴ 768 = CP × [ (100 – 20) /100 ]

∴ CP = [ 768 × 100 ] / 80 = 960

For gain of 20%, we should now calculate the selling price

∴ SP = CP [ (100 + gain%) / 100]

= 960 [ (100 + 20) /100 ] = 960 × (120 / 100)

= 96 × 12 =  ₹ 1152

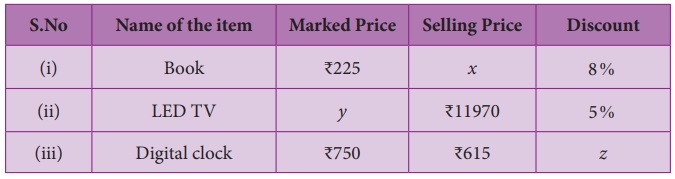
7. Find the unknowns x, y and z.

Solution 1:

Solution 2:

(i) Book marked price = ₹225 discount = 8%

∴  Selling price (x) = Marked price × [ (100 – d%) / 100 ]

= 225 × [ (100 – 8) / 100] = 225 × [92 / 100] = ₹ 207

(ii) LED TV selling price = 11970 discount = 5%, Marked price = y

∴ Selling price = Marked price y × [(100 – d%) / 100]

∴ 11970 = y × [ (100 – 5) / 100 ]

∴  y = [11970 × 100] / 95 = 126 × 100 = ₹ 12,600

(iii) Digital clock marked price (MP) = ₹ 750, MP = ₹ 12,600

Selling price (SP) = ₹ 615, Discount = z

SP = MP × [ (100 – d%) / 100 ]

∴ 615 = 750 × [ (100 – z) / 100 ]

∴  (100 − z) = [615 × 100] / 750

∴ 100 – z  =  82

∴  z = 100 − 82, Discount = 18%

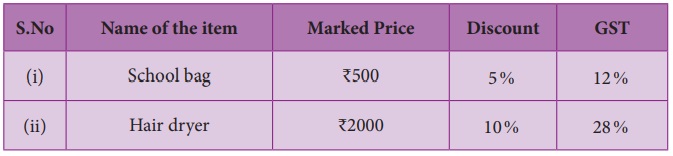
8. Find the total bill amount for the data given below:

Solution 1:

Solution 2:

Formula for discounted price DP = Marked price (MP) ×  [ (100 – d%) / 100 ]

When d is the discount %

  ∴ DP = MP × [(100 – d%) / 100]

(i) School bag = MP × [(100 – d%) / 100]

= 500 × [ (100 – 5) / 100 ] = [500 × 0.95] / 100 = ₹ 475

(ii) Hair drier = MP × [ (100 – d%) / 100 ]

= 2000 × [(100 – 10) / 100] = 2000 × 0.9 = ₹ 1,800

For bill amount, we should apply GST on the discounted value of the items.

Formula: Bill amount = Discounted price × [ (l00 + GST%) / 100 ]

  ∴ For (i) School bag,

Bill amount = 475 ×  [ (100 + 12) / 100 ] = 475 × 1.12 =  ₹ 532

  ∴  For (ii) Hair drier,

Bill amount = 1800 × [ (100 + 28) / 100 ] = 1800 × 1.28 = ₹ 2,304

∴  Total bill amount = Bill amount of School bag + Stationary + Cosmetics + Hair drier

= 532 + 2304

= ₹ 2,836

9. A branded Air-Conditioner (AC) has a marked price of ₹38000. There are 2 options given for the customer.

(i) Selling Price is the same ₹38000 but with attractive gifts worth ₹3000

(or)

(ii) Discount of 8% on the marked price but no free gifts. Which offer is better?

Solution:

Marked price of AC = ₹ 38,000

Option 1:

Selling price = ₹ 38000 & gifts worth ₹ 3000

Net gain for customer = ₹ 3000 as there is no discount on AC

Option 2:

Discount of 8%, but no gift

  ∴ Discounted value = MP × [ (l00 − d%) / 100 ]

= 38000 × [ (100 – 8) / 100 ] = 38000 × 0.92 = 34960

Savings for customer = 38000 – 34960 = ₹ 3040

Therefore, the customer gets 3000 gift in option 1 where as he is able to save only ₹ 3040 in option 2. Therefore, option 2 is better.

10. If a mattress is marked for ₹7500 and is available at two successive discounts of 10% and 20%, find the amount to be paid by the customer.

Solution:

Solution 2:

Marked price of mattress = ₹ 7500

Discount d₁ = 10%

Discount d₂ = 20%

Price after discount d₁  = MP × [ (100 − d₁%) / 100 ]

= 7500 × [ (100 − 10) / 100 ] = 7500 × 90/100 = 6750

Price after second discount d₂  = Discount price × [ (100 − d₂ %) / 100 ]

= 6750 × [ (100 − 20) / 100 ] = ₹ 5400

Objective Type Questions

11. A fruit vendor sells fruits for ₹200 gaining ₹40. His gain percentage is

(A)20%

(B) 22%

(C) 25%

(D) 16 2/3 %

[Answer: (C) 25%]

Solution:

Selling price = ₹ 200

Gain = 40

∴ CP = Selling price − gain = 200 – 40 = 160

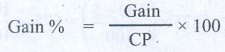
Gain % = [Gain / CP] × 100 = [40 / 160] × 100 = 25%

12. By selling a flower pot for ₹528, a woman gains 20%. At what price should she sell it to gain 25%?

(A) ₹500

(B) ₹550

(C) ₹553

(D) ₹573

[Answer: (B) ₹ 550]

Solution:

Solution 2:

If selling price (SP) =  ₹ 528

Gain % = 20%

∴ CP = ?

Selling price SP = CP × [ (100 + gain %) / 100 ]

∴ 528 = CP × [ (100 + 20) / 100 ]

∴  CP = [528 × 100] / 120 = 440

If gain % = 25%, Selling price?

Selling price SP = CP × [ (100 + gain%) / 100 ]

= 440 × [ (100 + 25) / 100 ] = 440 × [125 / 100] =  ₹ 550

13. A man buys an article for ₹150 and makes overhead expenses which are 12% of the cost price. At what price must he sell it to gain 5%?

(A) ₹180

(B) ₹168

(C) ₹176.40

(D) ₹88.20

[Answer: (C) 176.40]

Solution:

Cost price of article = ₹ 150

Over head expenses = 12% of cost price

= (12 / 100) × 150 = ₹ 18

∴ Effective cost of article = 150 + 18 = ₹ 168

Now, to gain 5%, he has to sell at

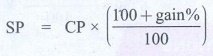
SP = CP × [ (100 + gain%) / 100]

= 168 × [ (100 + 5) / 100] = 168 × 1.05 = 176.40

14. What is the marked price of a hat which is bought for ₹210 at 16% discount?

(A) ₹243

(B) ₹176

(C) ₹230

(D) ₹250

[Answer: (D) ₹ 250]

Solution:

Solution 2:

Let marked price be MP

Discounted price = ₹ 210

Rate of discount =  16%

As per formula :

Discounted price = MP × [ (100 – d%) / 100 ]  = (100 – 16) / 100

MP = [210 × 100] / 84 = 250

15. The single discount in % which is equivalent to two successive discounts of 20% and 25% is

(A) 40%

(B) 45%

(C) 5%

(D) 22.5%

[Answer: (A) 40%]

Solution:

Solution 2:

Let marked price be MP, after discount 1 of 20%,

Discounted price = MP × [ (100 – d₁%) / 100 ] = [100 – 20] / 100 =  MP × [80/100]

After discount 2 of 25%,

Discounted price = Discounted price × [ (100 – d₂%) / 100 ]

= MP × 80/100 × [ (100 – 25) / 100 ]

= MP × [ (80  × 75) / (100 × 100) ] = MP × (60 / 100)

= MP × [ (100 – 40) / 100 ]  60 can be written as 100 − 40

Comparing with formula, we get

∴  This is equivalent to a single discount of 40%

Answer:

Exercise 4.2

1. (i) Cost price (ii) ₹7000 (iii) ₹600 (iv) 8% (v) ₹945

2. ₹902

3. ₹670

4. 50%

5. 11 (1/9) %

6. ₹1152

7. (i) x = ₹207 (ii) y = ₹12600 (iii) z = 18%

8. ₹2836

9. Discount of 8% is better

10. ₹5400

11. (C) 25%

12. (B) 550

13. (B) 168

14. (D) ₹250

15. (A) 40%