Exercise 4.1 (Percentage)

Exercise 4.1

1. Fill in the blanks:

(i) If 30 % of x is 150, then x is _________. [Answer: 500]

Solution:

Given 30% of x is 150

i.e 30/100 × x = 150

  ∴ x = [150 × 100] / 30

  ∴ x = 500

(ii) 2 minutes is _________ % to an hour. [Answer: 3 1/3 %]

Solution:

Let 2 min be x % of an hour

and 1 hr = 60 min

x % = (2/60) × 100 = 200 / 60 = 10 / 3 = 3 (1/3)

x = 3 (1/3)%

(iii) If x % of x = 25, then x = ________. [Answer: 50]

Solution:

Given that x % of x is 25

  ∴ [x / 100] × x =  25

∴ x² = 25 × 100 = 2500

∴ x = √2500 = 50

(iv) In a school of 1400 students, there are 420 girls. The percentage of boys in the school is ________. [Answer: 70]

Solution:

Given total number of students in school = 1400

Number of girls in school = 420

∴ Number of boys in school = 1400 − 420 = 980

% of boys in school = [ Number of boys / Total number of students ] × 100 = [ 980 / 1400 ] × 100

= 980 / 14 = 70

% of boys = 70%

(v) 0.5252 is ________ % . [Answer: 52.52%]

Solution:

Given a number, and to express as a percentage, we need to multiply by 100

∴ to express 0.5252 as percentage, we should multiply by 100

∴ 0.5252 × 100 = 52.52%

2. Rewrite each underlined part using percentage language.

(i) One half of the cake is distributed to the children.

Solution:

One half is nothing but 1/2

as percentage, we need to multiply by 100

∴ 1/2 × 100 = 50%

[Answer: 50% of the cake is distributed to the children]

(ii) Aparna scored 7.5 points out of 10 in a competition.

Solution:

7.5 points out of 10 is 7.5/10 = 0.75

For percentage, we need to multiply by 100

∴  We get 0.75 × 100 = 75% 

[Answer: Aparna scored 75% in a competition]

(iii) The statue was made of pure silver.

Solution:

Pure silver means there are no other metals

so,100 out of 100 parts is made of silver = 100/100

∴   to express as percentage, [100 / 100] × 100% = 100%

[Answer: The statue was made of 100% silver ]

(iv) 48 out of 50 students participated in sports.

48 out of 50 students in fraction form is 48/50.

As a percentage, we need to multiply by 100

∴ [48/50] × 100 = 96%

[Answer: 96% students participated in sports]

(v) Only 2 persons out of 3 will be selected in the interview.

Solution:

2 out of 3 in fraction form is 2/3

to express as percentage, we need to multiply by 100

(2/3) × 100 = 200/3  = 66 2/3%

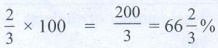
[Answer: only 66 2/3% persons will be selected in the interview]

3. 48 is 32% of which number?

Solution:

Let the number required to be found be ‘x’

Given that 32% of x is 48

ie (32/100) × x = 48 ∴ x = [48 × 100] / 32 = 300 / 2 = 150 ∴ x =  150

4. What is 25% of 30% of 400?

Solution:

Required to find 25% of 30% of 400

First 30% of 400 = [30/100] × 400 = 120

Next 25% of the above is = [25/100] × 120 = 30

5. If a car is sold for ₹200000 from its original price of ₹300000, then find the percentage of decrease in the value of the car.

Solution:

original price of car = ₹ 3,00,000

actual selling price of car = ₹ 2,00,000

Decrease in amount from original = 3,00,000 − 2,00,000 = 1,00,000

Percentage decrease = [ Decrease / Original value ] × 100 = [ 1,00,000 / 3,00,000 ] × 100 = 100 / 3 = 33 1/3%

6. If the difference between 75% of a number and 60% of the same number is 82.5, then find 20% of that number.

Solution:

Given that 75% of number less 60% of number is 82.5

Let the number be ‘x’

∴  (75/100) × x – (60/100) × x = 82.5

∴  0.75 x – 0.60 x = 82.5

∴ 0.15 x = 82.5

∴ x = 82.5 / 0.15 = 8250 / 15 = 550

Required to find 20% of number ie 20% of x.

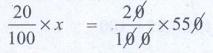
(20/100) × x = (20/100) × 550 = 110

7. A number when increased by 18% gives 236. Find the number.

Solution 1:

Let the number be x. Given that when it is increased by 18%, we get 236.

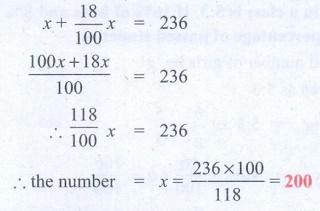
Solution 2:

Let the number be x. Given that when it is increased by 18%, we get 236.

x + (18/100)x = 236

( 100x + 18x ) / 100 = 236

∴  118/100 x = 236

∴  the number = x =  [236 × 100] / 118 = 200

8. A number when decreased by 20% gives 80. Find the number.

Solution 1:

Let the number be x. Given that when it is increased by 20% we get 80.

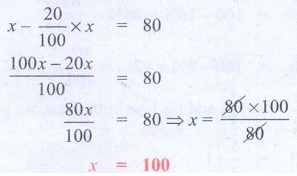
Solution 2:

Let the number be x. Given that when it is increased by 20% we get 80.

x – [ (20/100) × x ] = 80

[100x – 20x] / 100 = 80

80x / 100 = 80 ⇒ x = [80 × 100] / 80

x = 100

9. A number is increased by 25% and then decreased by 20%. Find the percentage change in that number.

Solution:

Method 1

Let the number be x.

First it is increased by 25%

∴  It becomes x + (25/100) × x = (125/100) x

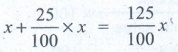
Secondary it is decreased by 20%

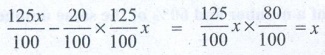
[125x / 100] – [20 / 100] × [125/100]x = [125/100]x × [80/100] = x

Now we get back x, therefore there is no change.

Hence percentage change in that number is 0%

Method 2

[to understand, let us assume that number is 100]

So, first when we increase by 25%, we get

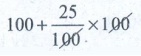
100 + ( [25 /100] × 100 ) = 100 +25 = 125

Now this 125 is decreased by 20%, we get

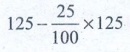
125 – ([25/100] × l25) = 125 − 25 = 100

∴  We get back 100 ⇒ No change

Hence percentage change in that number is 0%

10. The ratio of boys and girls in a class is 5:3. If 16% of boys and 8% of girls failed in an examination, then find the percentage of passed students.

Solution 1:

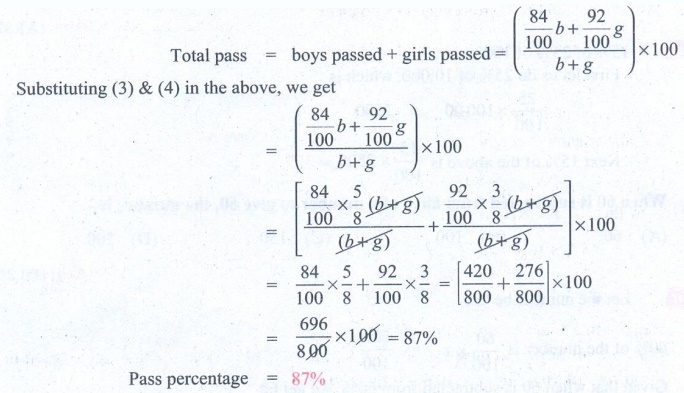
Solution 2:

Let number of boys be ‘b’ and number of girls be ‘g’

Ratio of boys and girls is given as 5:3

b:g = 5:3 ⇒ b/g = 5/3       ……..(A)

Failure in boys = 16% = 16/100 × b = 16b / 100

Failure in girls = 8% = 8/100 × g = 8g/100

Pass in boys = 100 − 16% = 84% = 84/100 b ……..(1)

Pass in girls = 100 − 8% = 92% = 92/100 g ……..(2)

From A, we have b/g = 5/3, adding 1 on both sides, we get

b/g + 1 = 5/3 + 1

[b + g ] / g = [5 + 3] / 3 = 8/3

∴  g = 3/8  (b + g )   ……..(3)

Similarly b = 5/8 (b + g ) ……..(4)

Total pass = Pass in girls / Pass in boys

= (1) + (2) = (84/100) b  + (92/100) g

Total pass percentage = [ Total pass / Total students ] × 100

Total pass = boys passed + girls passed = {[(84/100)b + (92/100)g ] / [b + g]} × 100

Substituting (3) & (4) in the above, we get

= {[(84/100)b + (92/100)g ] / [b + g]} × 100

= { [ ( 84/100 × 5/8(b + g) ) / (b + g)] + [ (92/100 × 3/8 (b + g) ) / (b + g) ] } × 100

= [ 84/100 × 5/8 ] + [ 92/100 × 3/8 ] = [420/800 + 276/800] × 100

= 696/800 × 100 = 87%

Pass percentage = 87%

Objective Type Questions

11. 12% of 250 litre is the same as ________of 150 litre.

(A) 10%

(B) 15%

(C) 20%

(D) 30%

[Answer: (C) 20%]

Solution:

12% of 250 = 12/100 × 250 = 30 lit.

Percentage : 30/100 × 100 = 20%

12. If three candidates A, B and C in a school election got 153,245 and 102 votes respectively, then the percentage of votes got by the winner is___________.

(A) 48%

(B) 49%

(C) 50%

(D) 45%

[Answer: (B) 49%]

Solution:

Candidate 1: 153

Candidate 2: 245 − winner [as maximum votes]

Candidate 3: 102

Total votes = 1 + 2 + 3 = 153 + 245 + 102 = 500

% of votes for winner = [ no. of votes that winner got / total votes ] × 100

= [245 / 500] × 100 = 49%

13. 15% of 25% of 10000 =___________.

(A) 375

(B) 400

(C) 425

(D) 475

[Answer: (A) 375]

Solution:

15% of 25% of 10000 is

First let us do 25% of 10,000, which is

[25/100] × 10000 = 2500

Next 15% of the above is [15/100] × 2500 = 375

14. When 60 is subtracted from 60% of a number to give 60, the number is

(A) 60

(B) 100

(C) 150

(D) 200

[Answer: (D) 200]

Solution:

Let the number be ‘x’

60% of the number is (60/100) × x = 60x / 100

Given that when 60 is subtracted from 60%, we get 60

i.e (60/100)x − 60 = 60

∴  (60/100)x = 60 + 60 = 120

∴ x = [120 × 100] / 60 = 200

15. If 48% of 48 = 64% of x , then x =

(A) 64

(B) 56

(C) 42

(D) 36

[Answer: (D) 36]

Solution:

Given that 48% of 48 = 64% of x

[48/100] × 48 = [64/100] × x

x = [48 × 48] / 64 = 36

x = 36

Answer:

Exercise 4.1

1. (i) x = 500 (ii) 3 1/3 % (iii) x = 50 (iv) 70% (v) 52.52%

2. (i) 50% (ii) 75% (iii) 100% (iv) 96% (v) 66 2/3%

3. x = 150

4. 30

5. 33 1/3%

6. 110

7. x = 200

8. x = 100

9. No change

10. 87%

11. (C) 20%

12. (B) 49%

13. (A) 375

14. (D) 200

15. (D) 36