Exercise 4.3 (Compound Interest)

Exercise 4.3

1. Fill in the blanks:

(i) The compound interest on ₹5000 at 12 % p.a for 2 years, compounded annually is ____________. [Answer: ₹  1272]

Solution:

Solution 2:

Compound Interest (CI) formula is

CI = Amount − Principal

Amount = A (1 + [r/100] )ⁿ

= 5000 ( 1 + 12/100 )² = 5000 × (112 / 100)² = 6272

∴ CI = 6272 – 5000 =   ₹ 1272

(ii) The compound interest on ₹8000 at 10 % p.a for 1 year, compounded half yearly is ____________. [Answer: ₹ 820 ]

Solution:

Solution 2:

Compound Interest (CI) = Amount − Principal

Amount = P (1 + [r/100] )²ⁿ [2n as it is compounded half yearly]

r = 10% p.a, for half yearly r = 10/2 = 5

∴ A = 8000 (1 + [5/100])^2x1 = 8000 × (105 / 100)² = 8820

CI = Amount – Principal = 8820 − 8000 = ₹  820

(iii) The annual rate of growth in population of a town is 10 % . If its present population is 26620, then the population 3 years ago was_________. [Answer: ₹ 20,000]

Solution:

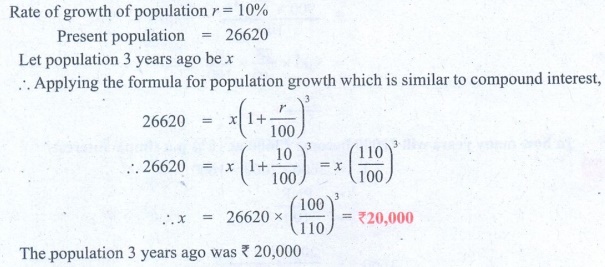
Solution 2:

Rate of growth of population r = 10%

Present population = 26620

Let population 3 years ago be x

∴ Applying the formula for population growth which is similar to compound interest,

26620 = x (1 + [r/100])³

∴ x = 26620 = x (1 + [10/100])³ = x (110/100)³

∴ x = 26620 × (110/100)³ =  ₹ 20,000

The population 3 years ago was  ₹ 20,000

(iv) If the compound interest is calculated quarterly, the amount is found using the formula __________. [Answer: 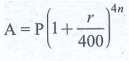[or] A = P ( 1 + r/400 )⁴ⁿ]

Solution:

Quarterly means 4 times in a year.

∴ The formula for compound interest is

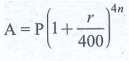
A = P ( 1 + r/400 )⁴ⁿ

(v) The difference between the C.I and S.I for 2 years for a principal of ₹5000 at the rate of interest 8 % p.a is ___________. [Answer: ₹ 32]

Solution:

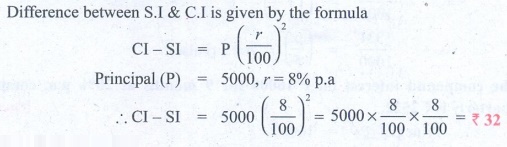
Solution 2:

Difference between S.I & C.I is given by the formula

CI − SI = P(r/100)²

Principal (P) = 5000, r = 8% p.a

∴ CI − SI =  5000 (8/100)² = 5000 × 8/100 × 8/100 = ₹ 32

2. Say True or False.

(i) Depreciation value is calculated by the formula, 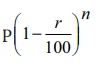 [Answer: True]

Solution:

Depreciation formula is P ( 1 – r/100 )ⁿ

(ii) If the present population of a city is P and it increases at the rate of r % p.a, then the population n years ago would be 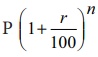. [Answer: False]

Solution:

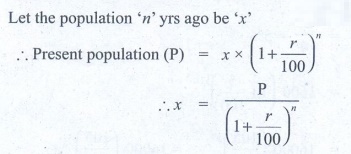
Solution 2:

Let the population 'n’ yrs ago be 'x'

∴ Present population (P) = x ×  ( 1 + [r/100] )ⁿ 

∴ x = P / (1 + [r/100])ⁿ 

(iii) The present value of a machine is ₹16800. It depreciates at 25 % p.a. Its worth after 2 years is ₹9450.  [Answer: True]

Solution:

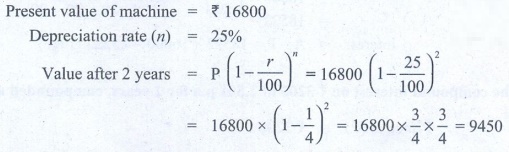
Solution 2:

Present value of machine = ₹ 16800

Depreciation rate (n) = 25%

Value after 2 years = P ( 1 + r/100 )ⁿ  = 16800 (1 – 25/100)²

= 16800 × ( 1 – 1/4 )² = 16800 × 3/4 × 3/4 =  9450

(iv) The time taken for ₹1000 to become ₹1331 at 20 % p.a, compounded annually is 3 years. [Answer: False]

Solution:

Solution 2:

Principal money = 1000

rate of interest = 20%

Amount (A) = 1331, applying in formula we get

A = (1 + [r/100] )ⁿ

∴1331 = 1000 (1 + [20/100] )ⁿ

1331/1000 = (1 + 1/5)ⁿ

1331/1000 = (6/5)ⁿ       ∴ n ≠ 3 (False)

(v) The compound interest on ₹16000 for 9 months at 20 % p.a, compounded quarterly is ₹2522.  [Answer: True]

Solution:

Solution 2:

Principal (P) = 16000

n = 9 months = 9/12 years

r = 20% p.a

For compounding quarterly, we have to use below formula.

Amount (A) = P × ( 1 + [r/100] )⁴ⁿ

Since quarterly we have to divide ‘r’ by 4

r = 20/4 = 5%

A = 16000 ( 1 + [5/100] )^9/12x4

= 16000 (105/100) ^9/12x4 = 16000 (105/100) ^9/3

= 16000 × (21/20)³ = 16000 × 21/20 × 21/20 × 21/20

∴  Interest = A − P = 18522 − 16000 = 2522 (True)

3. Find the compound interest on ₹3200 at 2.5 % p.a for 2 years, compounded annually.

Solution:

Solution 2:

Principal (P) = ₹ 3200

r = 2.5% p.a

n = 2 years comp, annually

∴ Amount (A) = (1 + [r/100] )ⁿ

= 3200 ( 1 + [2.5/100] )²

= 3200 × (1.025)² = 3362

Compound Interest (CI) = Amount − Principal

= 3362 – 3200 = ₹ 162

4. Find the compound interest for 2 1/2 years on ₹4000 at 10 % p.a, if the interest is compounded yearly.

Solution:

Solution 2:

Principal (P) =  ₹ 4000

r = 10% p.a

Compounded yearly

n = 2 1/2 years. Since it is of the form a b/c years

Amount (A) = (1 + [r/100] )^a ( 1 + ([b/c × r] / 100) )¹

= 4000 × (1 + 10/100)² ( 1 + [ (1/2 × 10) / 100] )¹

= 4000 × (110 / 100)² × (105 / 100)¹

= 4000 × 1.1 × 1.1 × 1.05 = 5082

∴ CI = Amount − Principal = 5082 – 4000 = 1082

5. A principal becomes ₹2028 in 2 years at 4 % p.a compound interest. Find the principal.

Solution:

Solution 2:

n = 2 years

r = rate of interest = 4% p.a

Amount A=  ₹ 2028

Amount (A) = P ( 1 + [r/100] )ⁿ   (Applying in formala]

2028 = P ( 1 + [4/100] )²

2028 = P (104/100)²

∴ P = [ 2028 × 100 × 100] / [104 × 104] =  ₹ 1875

6. In how many years will ₹3375 become ₹4096 at 13 1/3 % p.a if the interest is compounded half-yearly?

Solution:

Solution 2:

Principal =  ₹ 3375

Amount =  ₹ 4096

r = 13 1/3 % p.a = 40/3 % p.a 

Compounded half yearly r = [40/3] / 2 = 20 / 3 % half yearly

Let no. of years be n for compounding half yearly, formula is

A = P ( 1 + [r/100] )²ⁿ

∴ 4096 = 3375 ( 1 + [20/3 / 100] )²ⁿ

∴ 4096 / 3375 = (1 + [ 20 / (3×100) ] )²ⁿ = (1 + 1/15)²ⁿ

( [15 + 1] / 15)²ⁿ = (16/15)²ⁿ ⇒ ∴ 4096 / 3375 = (16/15)²ⁿ

Taking cubic root on both sides.

(16/15)^2n/3 = ³√4096 / ³√3375 = 16/15

∴ 2n/3 = 1  

∴ n = 3 / 2 = 1.5 years or 1 ½ years

7. Find the C.I on ₹15000 for 3 years if the rates of interest are 15 % , 20 % and 25 % for the I, II and III years respectively.

Solution:

Solution 2:

Principal (P) = ₹ 15000

rate of interest 1 (a) = 15% for year I

rate of interest 2 (b) = 20% for year II

rate of interest 3 (c) = 25% for year III

Formula for amount when rate of interest is different for different years is

A = (1 + a/100)¹ (1 + b/100)¹(1 + c/100)¹ 

Substituting in the above formula, we get

A = 15000 (1 + 15/100) (1 + 20/100) ( 1 + 25/100) 

= 15000 × 115/100 × 120/100 × 125/100 = 25,875

Compound Interest (CI) = A – P = 25,875 – 15,000 =  ₹ 10,875

CI = ₹ 10,875

8. Find the difference between C.I and S.I on ₹5000 for 1 year at 2 % p.a, if the interest is compounded half yearly.

Solution:

Solution 2:

Principal (P) = ₹ 5000

time period (n) = 1 yr.

Rate of interest (r) = 2% p.a

for half yearly r = 1%

Difference between CI & SI is given by the formula.

CI − SI = P (r/100)²ⁿ                [for half yearly compounding]

∴  CI − SI = 5000 (1/100)^2x1 = 5000 × 1/100 × 1/100 = ₹ 0.50

9. Find the rate of interest if the difference between C.I and S.I on ₹8000 compounded annually for 2 years is ₹20.

Solution:

Solution 2:

Principal (P) = ₹ 8000

time period (n) = 2 yrs.

rate of interest (r) = ?

Difference between CI & SI is given by the formula

CI − SI = P ^(1+r/100)n     

Difference between CI & SI is given as 20

∴  20 = 8000 × (r/100)²

∴ (r/100)² = 20/8000 = 1/400

Taking square root on both sides

r/100 = √[1/400] = 1/20

∴ r = 100 / 20 = 5%

10. Find the principal if the difference between C.I and S.I on it at 15 % p.a for 3 years is ₹1134.

Solution:

Solution 2:

Rate of interest (r) = 15% p.a

time period (n) =  3 years

Difference between CI & SI is given as 1134

Principal = ? → required to find

Using formula for difference

C.I − S.I = P(r/100)² (3 + r/100)

1134 = P(15/100)² (3 + 15/100)

1134 = P(0.15)² ([300 + 15]/100)

1134 = P (0.0225 × [315/100])

1134 = P × 0.070875

P = 1134/0.070875

P = ₹ 16,000

Objective Type Questions

11. The number of conversion periods in a year, if the interest on a principal is compounded every two months is___________.

(A) 2

(B) 4

(C) 6

(D) 12

[Answer: (C) 6]

Solution:

Conversion period is the time period after which the interest is added to the principal. If principal is compounded every two months then in a year, there will be 6 (12/2) conversion periods.

12. The time taken for ₹4400 to become ₹4851 at 10 % , compounded half yearly is _______.

(A) 6 months

(B) 1 year

(C) 1 years

(D) 2 years

[Answer: (B) 1 year]

Solution:

Solution 2:

Principal = ₹ 4400

Amount = ₹ 4851

Rate of interest = 10% p.a

for half yearly, divide by 2,

r = 10/2 = 5%

Compounded half yearly, so the formula is

A = P (1 + [r/100])²ⁿ

Substituting in the above formula, we get

4851 = 4400 (1 + [5/100])²ⁿ = 4400 ( [100 + 5] / 100 )²ⁿ

∴  4851/4400 =  (105/100)²ⁿ = (21/20)²ⁿ

(21/20)²ⁿ = 4851/4400 = [11 × 441] / [11 × 400] = 441/400

Taking square root on both sides, we get

(21/20)²ⁿ = (21/20)²

Equating power on both sides

∴ 2n = 2, n = 1

13. The cost of a machine is ₹18000 and it depreciates at 16 2/3 % annually. Its value after 2 years will be___________.

 (A) ₹12000

(B) ₹12500

(C) ₹15000

(D) ₹16500

[Answer: (B) ₹ 12500]

Solution:

Solution 2:

Cost of machine = ₹ 18000

Depreciation'rate = 16 2/3 % = 50/3 % p.a

time period = 2 years

∴  As per depreciation formula,

Depriciated value = Original value (1 – r/100]ⁿ

Substituting in above formula, we get

Depreciated value after 2 years = 18000 (1 – [(50/3) / 100] )² = 18000 (1 – [50/ (100 × 3)] )²

= 18000 (1 − 1/6)² = 18000 × (5/6)²

= 18000 × 5/6 × 5/6 = ₹ 12,500

14. The sum which amounts to ₹2662 at 10 % p.a in 3 years, compounded yearly is_______.

(A) ₹2000

(B) ₹1800

(C) ₹1500

(D) ₹2500

[Answer: (A) ₹ 2000]

Solution:

Solution 2:

Amount = ₹ 2662

Rate of interest = 10% p.a

Time period = 3 yrs. Compounded yearly

Principal (P) → required to find?

Applying formula A = P (1 + [r/100])ⁿ

2662 = P ( 1 + [10/100] )³ = P ( [100 + 10] / 100 )³

2662 = P (110/100)³ = 2662 = P(11/10)³

∴  P = [ 2662 × 10 × 10 × 10 ] / [ 11 × 11 × 11 ] = 2 × 10 × 10 × 10 =  ₹ 2000

15. The difference between compound and simple interest on a certain sum of money for 2 years at 2 % p.a is ₹1. The sum of money is __________ .

(A) ₹2000

(B) ₹1500

(C) ₹3000

(D) ₹2500

[Answer: (D) ₹ 2500]

Solution:

Solution 2:

Difference between CI and SI is given as Re 1

Time period (n) = 2 yrs.

Rate of interest (r) = 2% p.a

Formula for difference is

CI − SI = P ×  (1 + r/100)ⁿ

Substituting the values in above formula, we get

1 = P × (2/100)²

∴  P = 1 × (100/2)² = 1 × (50)² = ₹ 2500

Answer:

Exercise 4.3

1. (i) ₹1272 (ii) ₹820 (iii) ₹20,000 (iv) A = P (1 + [r/400])⁴ⁿ (v) ₹32

2. (i) True (ii) False (iii) True (iv) False (v) True

3. ₹162

4. ₹936.80

5. ₹1875

6. 1 1/2 years

7. ₹10,875

8. ₹0.50

9. 5%

10. ₹ 16000

11. (C) 6

12. (B) 1 year

13. (B) ₹ 12500

14. (A) ₹2000

15. (D) ₹2500