Exercise 4.5

Exercise 4.5

Miscellaneous Practice Problems

1. A fruit vendor bought some mangoes of which 10% were rotten. He sold 33 1/3 % of the rest. Find the total number of mangoes bought by him initially, if he still has 240 mangoes with him.

Solution:

Solution 2:

Let the number of mangoes bought by fruit seller initially be x.

Given that 10% of mangoes were rotten

∴ Number of rotten mangoes = (10/100) × x

Number of good mangoes = x  − no. of rotten mangoes

= x – [10/100]x = [100x – 10x ] / 100 = [90/100] x …….(1)

Number of mangoes sold = 33 (1/3)% of good mangoes = 100/3%

∴  Mangoes sold = [100/3] × [90/100]x × [1/100] = [30/100] x…….(2)

Number of mangoes remaining = No of good mangoes − No. of mangoes sold

From (1) and (2)

∴  [90 /100]x – [30/100]x = 240 ⇒ [90x − 30x ] / 100 = 240

∴  60x /100 = 240

∴ x  = [240 × 100] / 60

x  = 400

∴ Initially he had 400 mangoes

2. A student gets 31 % marks in an examination but fails by 12 marks. If the pass percentage is 35 % , find the maximum marks of the examination.

Solution:

Solution 2:

Let the maximum marks in the exam be ‘x’

Pass percentage is given as 35%

∴  Pass mark = [35/100] × x = [35/100]x

Student gets 31 % marks = [31 /100] × x = [31/100] x

But student fails by 12 marks → meaning his mark is 12 less than pass mark.

∴ [31/100] x = [35 / 100] x − 12

∴ [35/100] x – [31/100] x = 12

∴  [35x − 31x ] / 100 = 12  ⇒ 4x / 100 = 12

∴  x = [12  × 100] / 4 = 300

Maximum mark is 300

3.  Sultana bought the following things from a general store. Calculate the total bill amount paid by her.

(i) Medicines costing ₹800 with GST at 5 %

(ii) Cosmetics costing ₹650 with GST at 12 %

(iii) Cereals costing ₹900 with GST at 0 %

(iv) Sunglass costing ₹1750 with GST at18 %

(v) Air Conditioner costing ₹28500 with GST at 28 %

Solution:

Solution 2:

Formula for bill amount is cost ( 1 + [GST % / 100] )

(i) Medicine : bill amount is 800 ( 1 + [5/100] ) = 800 × [105 / 100] = 840

(ii) Cosmetics: Bill amount is 650 ( 1 + [12 / 100] ) = 650 × [112 / 100] = 728

(iii) Cereals : Bill amount is 900 (1 + [0 / 100] ) = 900

(iv) Sunglass: bill amount is 1750 (1 + [18/100] ) = 1750 × [118/100] = 2065

(v) AC : Bill amount is 28500 (1 + [28/100]) = 28500 × [128/100] = 36480

∴  Total bill amount = 840 + 728 + 900 + 2065 + 36480

=  ₹ 41,013 (total bill amount)

4. P’s income is 25 % more than that of Q. By what percentage is Q’s income less than P’s?

Solution:

Let Q’s income be 100.

P’s income is 25% more than that of Q.

∴  P’s income = 100 + [ (25/100) × 100 ] = 125

Q’s income is 25 less than that of P

In percentage terms, Q’s income is less than P’s with respect to P’s income is

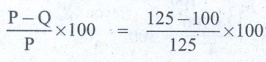
[(P – Q) / P] × 100 = [ (125 – 100) / 125] × 100 = [25 / 125] × 100 = 20%

5. Vaidegi sold two sarees for ₹2200 each. On one she gains 10 % and on the other she loses 12 % . Find her total gain or loss percentage in the sale of the sarees.

Solution:

Solution 2:

Saree 1 :

The selling price is ₹ 2200, let cost price be CP₁, gain is 10%

Cost price? Using the formula

SP = CP₁ (1 + [gain%/10] ) & substituting the values

2200 = CP₁ = ( 1 + [10/100] )  ∴  CP₁ = 2200 × [100/110]  = 2000

Saree 2:

The selling price is 2200, let cost price be CP₂, loss is given as 12%. We need to find CP₂ using the formula as before,

SP = CP₂ (1 + [loss%/100] ) & substituting the values

2200 = CP₂ (1 – [12/100] ) = CP₂  × ( [100–12] / 100)

= CP₂  × [88/100]

∴   CP₂  = [2200 × 100] / 88 = 2500

∴  Cost price of both together is CP₁ + CP₂

= 2000 + 2500 = 4500 …….. (1)

Selling price of both together is 2 × 2200 = 4400 …….. (2)

Since net selling price less than net cost price, there is a loss.

Loss %  =  [ loss / cost price ] × 100

Loss = Net cost price − Net selling price

(1) – (2) = 4500 – 4400 = 100

∴  Loss %  =  [100/4500] × 100 = 100/45 = 20/9 = 2 2/9 %

= 2 2/9 %

6. If 32 men working 12 hours a day can do a work in 15 days, then how many men working 10 hours a day can do double that work in 24 days?

Solution:

Let the required number of men be x.

x = 24 persons.

To complete the same work 24 men needed.

To complete double the work 24 × 2 = 48 men are required.

7. Amutha can weave a saree in 18 days. Anjali is twice as good a weaver as Amutha.If both of them weave together, then in how many days can they complete weaving the saree?

Solution:

Amutha can weave a saree in 18 days.

Anjali is twice as good as Amutha.

ie. If Amutha weave for 2 days, Anjali do the same work in 1 day.

If Anjali weave the saree she will take

18 / 2 = 9 days.

Hence time taken by them together

= ab / [a + b] days

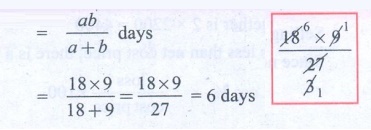
= [18 × 9] / [18 + 9] =  [18 × 9] / 27 = 6 days

In 6 days they complete weaving the saree.

8. P and Q can do a piece of work in 12 days and 15 days respectively. P started the work alone and then after 3 days, Q joined him till the work was completed. How long did the work last?

Solution:

Solution 2:

P can do a piece of work in 12 days.

∴ P's 1 day work = 1/12

P's 3 day's work = 3 × (1/12) = 3/12.

Q can do a piece of work in 15 days.

∴ Q's 1 day work = 1/15

Remaining work after 3 days = 1 – (3/12) = 9/12

(P + Q)'s 1 day work = 1/12 + 1/15 = 5/60 + 4/60 = 9/60.

∴ Number of days required to finish the remaining work

= Remaining work / (P + Q)'s 1 day work = [9/12] / [9/60] = [9/12] × [60/9] = 5

Remaining work lasts for 5 days

Total work lasts for 3 + 5 = 8 days.

Challenging Problems

9. If the numerator of a fraction is increased by 50 % and the denominator is decreased by 20 % , then it becomes 3/5. Find the original fraction.

Solution:

Solution 2:

Original fraction = x/y

numerator increased by 50%

∴ Numerator  = [150 / 100] x

Denominator decreased by 20%

∴  Denominator = [80/100] y

Hence

[ (150/100)x ] / [ (80/100)y ] = 3/5

[(15/10)x] / [(8/10) y ] = 3/5

[15x / 10] × [10 / 8x ] = 3/5

x/y = [3/5] × [8/15] = 8/25

10. Gopi sold a laptop at 12 % gain. If it had been sold for ₹1200 more, the gain would have been 20 % . Find the cost price of the laptop.

Solution:

Solution 2:

Let the cost price of the laptop be ‘x ’

Gain = 12%

∴  Selling price (SP) = CP (1 + [gain % / 100] )

Substituting in formula = x ( 1 + [12/100] ) = x ( [100 + 12]/100 ) = [112/100]x

If the selling price was 1200 more

i.e [112/100]x + 1200 , the gain is 20%

i.e new selling price = x (1 + [20/100] )

= [112/100] x + 1200 = x(100 + [20/100] ) = [120/100]x

∴  1200 = [120/100]x – [112/100]x = [8/100]x

∴ x = [1200 × 100] / 8 = 15000

Cost price of the laptop is ₹ 15,000/−

11. A shopkeeper gives two successive discounts on an article whose marked price is ₹180 and selling price is ₹108. Find the first discount percentage if the second discount is 25% .

Solution:

Solution 2:

Marked price is given as ₹ 180

Let 1^st discount be d₁% = ? (to find)

2^nd discount be d₂ % = 25%

Selling price is 108 (given)

Price after 1^st discount = 180 (1 – [d₁/100] ) = P₁ ………..(1)

Price after 2^nd discount = P₁ (1 – [d₂/100] ) = 108

Substituting for P₁ from (1), we get

180 (1 – [d₁/100] ) (1 – [d₂/100] )  = 108   ⇒ Since d₂ = 25, we get

180 (1 – [d₁/100] ) (1 – [25/100] )  = 108  

∴  (1 – [d₁/100] ) = [108/108] × [100 / 75] = 4/5

1 – [d₁/100] = 4/5

∴ d₁ / 100 = 1 – [4/5] = 1/5

∴  d₁ = [1/5] × 100 = 20%

1st  discount = 20%

12. Find the rate of compound interest at which a principal becomes 1.69 times itself in 2 years.

Solution:

Solution 2:

Let principal be ‘P’

Amount is given to be 1.69 times principal

i.e 1.69 P

Time period is 2yrs. = (n)

Rate of interest = r = ? (required)

Applying the formula,

Amount = Principal (1 + [r/100] )ⁿ

Substituting, 1.69 P = P (1 + [r/100])²

∴  (1 + [r/100] )² = 1.69P / P = 1.69

Taking square root on both sides, we get

√1.69 = 1 + [ r / 100 ]

∴  1 + [ r / 100] = 1.3

∴   r / 100 = 1.3

 r = 30%

∴   rate of compound interest is 30%

13. A small–scale company undertakes an agreement to make 540 motor pumps in 150 days and employs 40 men for the work. After 75 days, the company could make only 180 motor pumps. How many more men should the company employ so that the work is completed on time as per the agreement?

Solution:

Let the number of men to be appointed more be x.

To produce more pumps more men required

∴  It is direct variation.

∴  The multiplying factor is 360/180

More days means less employees needed.

∴  It is Indirect proportion.

∴  The multiplying factor is 75/75

Now 40 + x = 40 × [360/180] × [75/75]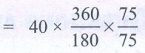 

40 + x = 80

x = 80 − 40

x = 40

40 more man should be employed to complete the work on time as per the agreement.

14. P alone can do 1/2 of a work in 6 days and Q alone can do 2/3 of the same work in 4 days. In how many days will they finish 3/4 of the work, working together?

Solution:

Solution 2:

1/2 of the work is done by P in 6 days

∴  Full work is done by P in [ 6 /(1/2) ] = 6 × 2 = 12 days

2/3 of work done by Q in 4 days.

∴ Full work done by Q in [ 4 / (2/3) ] = 4 × 3/2 = 6 days

(P + Q) will finish the whole wotk in ab / [a + b] days = [12 × 6] / [12 + 6] = [ 12 × 6] / 18 = 4 days

(P + Q) will finish 3/4 of the work in 4 × [3/4]  = 3 days.

15. X alone can do a piece of work in 6 days and Y alone in 8 days. X and Y undertook the work for ₹48000. With the help of Z, they completed the work in 3 days. How much is Z’s share?

Solution:

X can do the work in 6 days.

X's 1 day work = 1/6

X's share for 1 day = 1/6 × 48000 =  ₹ 8,000

X's share for 3 days = 3 × 8000 =  ₹ 24,000

Y can complete the work in 8 days.

Y's 1 day work = 1/8

Y's 1 day share = 1/8 × 48000 =  ₹ 6,000

Y's 3 days share =  ₹ 6000 × 3 =  ₹ 18,000

(X + Y)'s 3 days share =  ₹ 24,000 +  ₹ 18,000 =  ₹ 42,000

Remaining money is Z's share

∴  Z's share =  ₹ 48,000 −  ₹ 42,000 =  ₹ 6,000

Exercise 4.5

Miscellaneous Practice Problems

1. 400

2. 300

3. ₹38163

4. 20%

5. 2 2/9 % loss

6. 48 men

7. 6 days

8. 8 days

Challenging Problems

9. 8/25

10. ₹15000

11. 20 %

12. 30 %

13. 20 more men

14. 3 days

15. ₹ 6000