Chapter: Basic Electrical and electronics : Electrical Mechanics
Transformer on No Load and Load
Transformer on No Load.
When the primary of a transformer is connected to the source of an ac supply and the secondary is open circuited, the transformer is said to be on no load. The Transformer on No Load alternating applied voltage will cause flow of an alternating current I0 in the primary
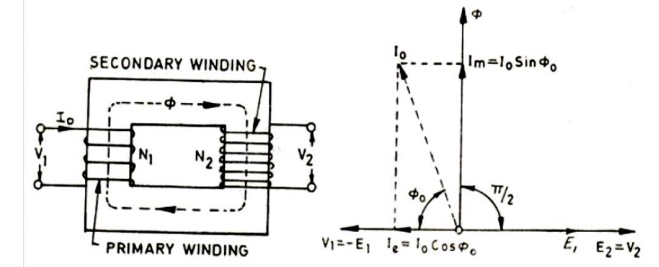
winding, which will create alternating flux Ø. No-load current I0, also known as excitation or exciting current, has two components the magnetizing component Im and the energy component Ie. Im is used to create the flux in the core and Ie is used to overcome the hysteresis and eddy current losses occurring in the core in addition to small amount of copper losses occurring in the primary only (no copper loss occurs in the secondary, because it carries no current, being open circuited.)
From vector diagram shown in above it is obvious that
1. Induced emfs in primary and secondary windings, E1 and E2 lag the main flux Ø by and are in phase with each other.
2. Applied voltage to primary V1 and leads the main flux Ø by and is in phase opposition to E1.
3. Secondary voltage V2 is in phase and equal to E2 since there is no voltage drop in secondary.
4. Im is in phase with Ø and so lags V1 by
5. Ie is in phase with the applied voltage V1.
6. Input power on no load = V1Ie = V1I0 cos Ø0 where Ø0 = tan-1
Transformer on Load:
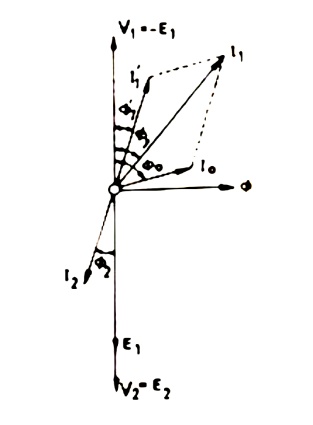
The transformer is said to be loaded, when its secondary circuit is completed through an impedance or load. The magnitude and phase of secondary current (i.e. current flowing through secondary) I2 with respect to secondary terminals depends upon the characteristic of the load i.e. current I2 will be in phase, lag behind and lead the terminal voltage V+2+ respectively when the load is non-inductive, inductive and capacitive. The net flux passing through the core remains almost constant from no-load to full load irrespective of load conditions and so core losses remain almost constant from no-load to full load. Vector diagram for an ideal transformer supplying inductive load is shown
Resistance and Leakage Reactance In actual practice, both of the primary and secondary windings have got some ohmic resistance causing voltage drops and copper losses in the windings. In actual practice, the total flux created does not link both of the primary and secondary windings but is divided into three components namely the main or mutual flux Ø linking both of the primary and secondary windings, primary leakage flux ØL1 linking with primary winding only and secondary leakage flux ØL2 linking with secondary winding only. The primary leakage flux ØL1 is produced by primary ampere-turns and is proportional to primary current, number of primary turns being fixed. The primary leakage flux ØL1 is in phase with I1 and produces self induced emf ØL1 is in phase with I1 and produces self induced emf EL1 given as 2f L1 I1 in the primary winding.
The self induced emf divided by the primary current gives the reactance of primary and is denoted by X1.
i.e. X1 = EL1/I1 = 2πfL1I1/I1 = 2FL1,
Similarly leakage reactance of secondary X2 = EL2/E2 = 2fπL2I2/I2 = 2πfL
Equivalent Resistance and Reactance. The equivalent resistances and reactance’s of transformer windings referred to primary and secondary sides are given as below Referred to primary side Equivalent resistance,
Equivalent resistance, = X'1 = Referred to secondary side Equivalent resistance,
Equivalent resistance, = X2 + K2X1 Where K is the transformation ratio.
Related Topics