EMF Equation of Transformer

EMF Equation of Transformer:

Let the applied voltage V1 applied to the primary of a transformer, with secondary open-circuited, be sinusoidal (or sine wave). Then the current I1, due to applied voltage V1, will also be a sine wave. The mmf N1 I1 and core flux Ø will follow the variations of I1 closely. That is the flux is in time phase with the current I1 and varies sinusoidally.

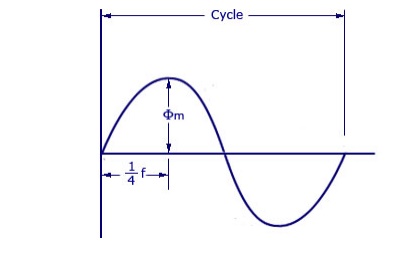
Let,

NA = Number of turns in primary NB = Number of turns in secondary

Ømax = Maximum flux in the core in webers = Bmax X A f = Frequency of alternating current input in hertz (HZ)

As shown in figure above, the core flux increases from its zero value to maximum value Ømax in one quarter of the cycle , that is in ¼ frequency second.

Therefore, average rate of change of flux = Ømax/ ¼ f = 4f ØmaxWb/s

Now, rate of change of flux per turn means induced electro motive force in volts. Therefore,

average electro-motive force induced/turn = 4f Ømaxvolt

If flux Ø varies sinusoidally, then r.m.s value of induced e.m.f is obtained by multiplying the average value with form factor.

Form Factor = r.m.s. value/average value = 1.11 Therefore, r.m.s value of e.m.f/turn = 1.11 X 4f Ømax = 4.44f Ømax 

Now, r.m.s value of induced e.m.f in the whole of primary winding

= (induced e.m.f./turn) X Number of primary turns

Therefore,

EA = 4.44f NAØmax = 4.44fNABmA

Similarly, r.m.s value of induced e.m.f in secondary is

EB = 4.44f NB Ømax = 4.44fNBBmA

In an ideal transformer on no load, VA = EA  and VB = EB  , where VB is the terminal voltage

Voltage Transformation Ratio.

The ratio of secondary voltage to primary voltage is known as the voltage transformation ratio and is designated by letter K. i.e.

Voltage transformation ratio, K = V2/V1 = E2/E1 = N2/N1

Current Ratio.

The ratio of secondary current to primary current is known as current ratio and is reciprocal of voltage transformation ratio in an ideal transformer.