Test of Hypotheses for Population Mean (Population Variance Is Known)

TEST OF HYPOTHESES FOR POPULATION MEAN (Population Variance Is Known)

Procedure:

Step 1 : Let µ and σ² be respectively the mean and the variance of the population under study, where σ² is known. If µ₀ is an admissible value of µ, then frame the null hypothesis as H₀: µ = µ₀ and choose the suitable alternative hypothesis from

(i) H₁: µ ≠ µ₀ (ii) H₁: µ > µ₀ (iii) H₁: µ < µ₀

Step 2 : Let (X ₁, X₂ , …, X_n) be a random sample of n observations drawn from the population, where n is large (n ≥ 30).

Step 3 : Let the level of significance be α.

Step 4 : Consider the test statistic 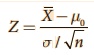 under H₀. Here,  represents the sample mean,  which is defined in  Note 2. The approximate sampling distribution of the test statistic under H₀ is the N(0,1) distribution.

Step 5 : Calculate the value of Z for the given sample (x₁, x₂, ..., x_n) as

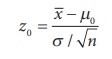
Step 6 : Find the critical value, z_e, corresponding to α and H₁ from the following table

Step 7 : Decide on H₀ choosing the suitable rejection rule from the following table corresponding to H₁.

Example 1.7

A company producing LED bulbs finds that mean life span of the population of its bulbs is 2000 hours with a standard derivation of 150 hours. A sample of 100 bulbs randomly chosen is found to have the mean life span of 1950 hours. Test, at 5% level of significance, whether the mean life span of the bulbs is significantly different from 2000 hours.

Solution:

Step 1 : Let μ and σ represent respectively the mean and standard deviation of the probability distribution of the life span of the bulbs. It is given that σ = 150 hours. The null and alternative hypotheses are

Null hypothesis: H₀: μ = 2000

i.e., the mean life span of the bulbs is not significantly different from 2000 hours.

Alternative hypothesis: H₁ : μ ≠ 2000

i.e., the mean life span of the bulbs is significantly different from 2000 hours.

It is a two-sided alternative hypothesis.

Step 2 : Data

The given sample information are

Sample size (n) = 100, Sample mean (x) = 1950 hours

Step 3 : Level of significance = 5%

Step 4 : Test statistic

The test statistic is , under H₀

Under the null hypothesis H₀, Z follows the N(0,1) distribution.

Step 5 : Calculation of Test Statistic

The value of Z under H₀ is calculated from

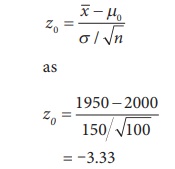
 = –3.33

Thus; |z₀| = 3.33

Step 6 : Critical value

Since H₁ is a two-sided alternative, the critical value at α = 0.05 is z_e = z_0.025 = 1.96.

(see Table 1.6).

Step 7 : Decision

Since H₁ is a two-sided alternative, elements of the critical region are determined by the rejection rule |z₀| ≥ z_e . Thus, it is a two-tailed test. For the given sample information, the rejection rule holds i.e., |z₀| = 3.33 > z_e = 1.96. Hence, H₀ is rejected in favour of H ₁: μ ≠ 2000. Thus, the mean life span of the LED bulbs is significantly different from 2000 hours.

Example 1.8

The mean breaking strength of cables supplied by a manufacturer is 1900 n/m² with a standard deviation of 120 n/m². The manufacturer introduced a new technique in the manufacturing process and claimed that the breaking strength of the cables has increased. In order to test the claim, a sample of 60 cables is tested. It is found that the mean breaking strength of the sampled cables is 1960 n/m². Can we support the claim at 1% level of significance?

Solution:

Step 1 : Let μ and σ represent respectively the mean and standard deviation of the probability distribution of the breaking strength of the cables. It is given that σ = 120 n/m². The null and alternative hypotheses are

Null hypothesis H₀: μ = 1900

i.e., the mean breaking strength of the cables is not significantly different from 1900n/m².

Alternative hypothesis: H₁: μ > 1900

i.e., the mean breaking strength of the cables is significantly more than 1900n/m².

It may be noted that it is a one-sided (right) alternative hypothesis.

Step 2 : Data

The given sample information are

Sample size (n) = 60. Hence, it is a large sample.

Sample mean ()= 1960

Step 3 : Level of significance

 α= 1%

Step 4 : Test statistic

The test statistic is 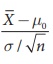, under H₀

Since n is large, under the null hypothesis, the sampling distribution of Z is the N(0,1) distribution.

Step 5 : Calculation of test statistic

The value of Z under H₀ is calculated from z₀ = 

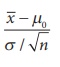
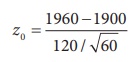
Thus, z₀ = 3.87

Step 6 : Critical value

Since H₁ is a one-sided (right) alternative hypothesis, the critical value at α = 0.01 level of significance is z_e = z_0.01= 2.33 (see Table 1.6)

Step 7 : Decision

Since H₁ is a one- sided (right) alternative, elements of the critical region are determined by the rejection rule z₀ > z_e. Thus, it is a right-tailed test. For the given sample information, the observed value z₀ = 3.87 is greater than the critical value z_e = 2.33. Hence, the null hypothesis H₀ is rejected. Therefore, the mean breaking strength of the cables is significantly more than 1900 n/m².

Thus, the manufacturer’s claim that the breaking strength of cables has increased by the new technique is found valid.