Test of Hypotheses for Equality of Proportions of two Populations

TEST OF HYPOTHESES FOR EQUALITY OF PROPORTIONS OF TWO POPULATIONS

Procedure:

Step 1 : Let P_X and P_Y denote respectively the proportions of Population-1 and Population-2 possessing the qualitative characteristic (attribute) under study. Frame the null hypothesis as H₀: P_X=P_Y and choose the suitable alternative hypothesis from

(i) H₁: P_X≠ P_Y (ii) H₁: P_X>P_Y (iii) H₁: P_X<P_Y

Step 2 : Let p _X and p_Y denote respectively the proportions of the samples of sizes m and n drawn from Population-1 and Population-2 possessing the attribute, where m and n are large (i.e., m ≥ 30 and n ≥ 30). Also, mp_X > 5, m (1- p_X) > 5, np_Y > 5 and n (1 - p_Y ) > 5 .

Here, these two samples are assumed to be independent.

Step 3 : Specify the level of significance, α.

Step 4 : Consider the test statistic 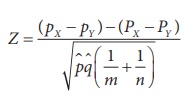 under H₀. Here, 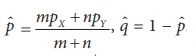. The approximate sampling distribution of the test statistic under H₀  is the N(0,1) distribution.

Step 5 : Calculate the value of Z for the given data as z₀ = .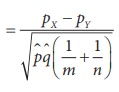

Step 6 : Choose the critical value, z_e, corresponding to α and H₁ from the following table

Step 7 : Decide on H₀ choosing the suitable rejection rule from the following table corresponding to H₁.

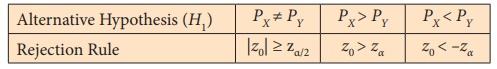
Example 1.13

A study was conducted to investigate the interest of people living in cities towards self-employment. Among randomly selected 500 persons from City-1, 400 persons were found to be self -employed. From City -2, 800 persons were selected randomly and among them 600 persons are self-employed. Do the data indicate that the two cities are significantly different with respect to prevalence of self-employment among the persons? Choose the level of significance as α = 0.05.

Solution:

Step1 : Let P_X and P_Y be respectively the proportions of self-employed people in City-1 and City-2. Then, the null and alternative hypotheses are

Null hypothesis: H₀ : P_X = P_Y

i.e., there is no significant difference between the proportions of self-employed people in City-1 and City-2.

Alternative hypothesis: H₁ : P_X ≠ P_Y

i.e., difference between the proportions of self-employed people in City-1 and City-2 is significant. It is a two-sided alternative hypothesis.

Step 2 : Data

The given sample information are

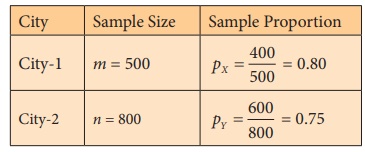
Here, m ≥ 30, n ≥ 30, mp_X = 400 > 5, m(1− p_X) = 100 > 5, np_Y = 600 > 5 and n(1− p_Y) = 200 > 5.

Step 3 : Level of significance

 α= 5%

Step 4 : Test statistic

The test statistic under the null hypothesis is

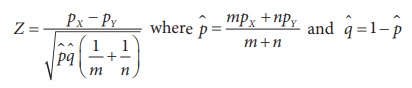
The sampling distribution of Z under H₀ is the N(0,1) distribution.

Step 5 : Calculation of Test Statistic

The value of Z for given sample information is calculated from

z₀ = 2.0764

Step 6 : Critical value

Since H₁ is a two -sided alternative hypothesis, the critical value at 5% level of significance is z_e = 1.96.

Step 7 : Decision

Since H₀ is a two-sided alternative, elements of the critical region are determined by the rejection rule |z₀| > z_e. Thus, it is a two-tailed test. For the given sample information, z_e = 2.0764 > z_e = 1.96. Hence, H₀ is rejected. We can conclude that the difference between the proportions of self-employed people in City-1 and City-2 is significant.