Definition, Example Solved Problems | Statistics - Standard Error | 12th Statistics : Chapter 1 : Tests of Significance - Basic Concepts and Large Sample Tests
Chapter: 12th Statistics : Chapter 1 : Tests of Significance - Basic Concepts and Large Sample Tests
Standard Error
STANDARD ERROR
The standard deviation of the sampling distribution of a statistic
is defined as the standard error of the statistic, which is abbreviated as SE.
For example, the standard deviation of the sampling distribution
of the sample mean, x, is known as the standard error of the sample
mean, or SE (
).
If the random variables X1, X2,
..., X–n are independent and have the same distribution with
mean μ and variance σ2, then variance of becomes as
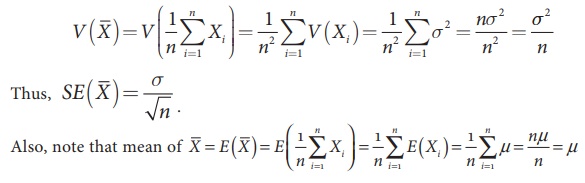
Example 1.2
Calculate the standard error of for the
sampling distribution obtained in Example 1.
Solution:
Here, the population is {4, 8, 12, 16}.
Population size (N) = 4, Sample size (n) = 2
Population mean (µ) = (4 + 8 + 12+ 16)/4 = 40/4 = 10
The population variance is calculated as
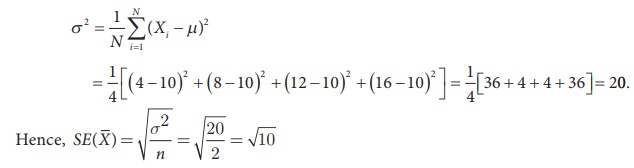
This can also be verified from the sampling distribution of (see Table 1.3)
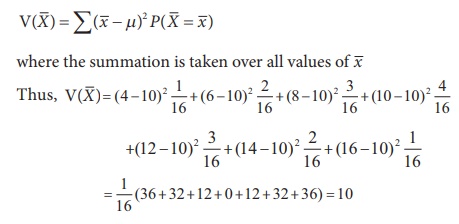
Hence, the standard deviation of the sampling distribution of is = √10 .
Standard Errors of some of the frequently referred statistics are
listed in Table 1.4.
Table 1.4 Statistics and their Standard Errors
Related Topics