Statistics - Sampling Distribution | 12th Statistics : Chapter 1 : Tests of Significance - Basic Concepts and Large Sample Tests
Chapter: 12th Statistics : Chapter 1 : Tests of Significance - Basic Concepts and Large Sample Tests
Sampling Distribution
SAMPLING DISTRIBUTION
The probability distribution of a statistic is called sampling distribution of the statistic. In
other words, it is the probability distribution of possible values of the
statistic, whose values are computed from possible random samples of same size.
The following example will help to understand this concept.
Example 1.1
Suppose that a population consists of 4 elements such as 4, 8, 12
and 16. These may be considered as the values of a random variable, say, X.
Let a random sample of size 2 be drawn from this population under sampling
with replacement scheme. Then, the possible number of samples is 42.
It is to be noted that, if we take samples of size n each from a
finite population of size N, then the number of samples will be Nn
under with replacement scheme and NCn samples under without replacement scheme.
In each of the 42 samples, the sample elements x
1 and x2 can be considered as the values of the
two iid random variables X1 and X2.
The possible samples, which could be drawn from the above population and their
respective means are presented in Table 1.2.
Table 1.2 Possible Samples and their Means
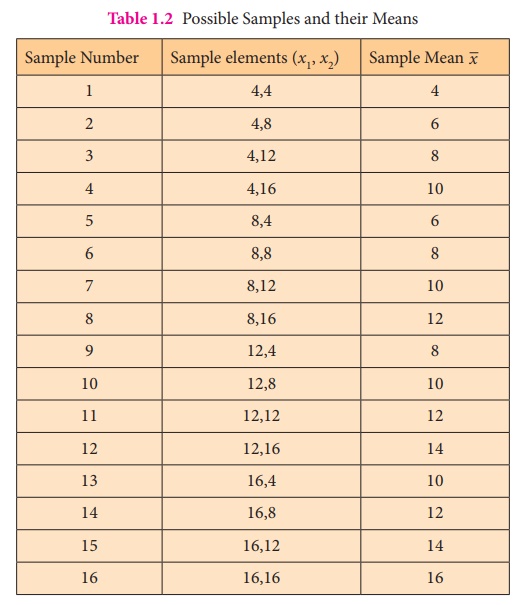
The set of pairs (x1, x2) listed in
column 2 constitute the sample space of samples of size 2 each.
Hence, the sample space is:
S = {(4,4), (4,8), (4,12),
(4,16), (8,4), (8,8), (8,12), (8,16), (12,4), (12,8), (12,12), (12,16), (16,4),
(16,8), (16,12), (16,16)}
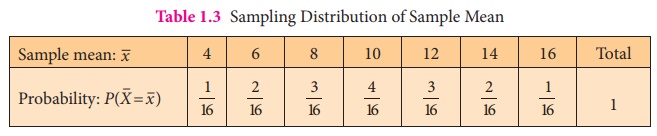
The sampling distribution of 
, the
sample mean, is determined and is presented in Table 1.3.
Note 4: The sample obtained under sampling with replacement from a finite population
satisfies
the conditions for a
random sample as described earlier.
Note 5: If the sample values are selected under without replacement
scheme,
independence property of X1, X2, ... Xn
will be violated. Hence it will not be a random sample.
Note 6: When the sample size is greater than or equal to 30, in most of
the text books, the sample is termed as a large sample. Also, the sample of size less than 30 is termed as small sample. However, in practice,
there is no rigidity in this number i.e., 30, and that depends on the
nature of the population and the sample.
Note 7: The learners may recall from XI Standard Textbook that some of the
probability distributions possess the additive property. For example, if X1,
X2, ..., Xn are iid N(μ, σ2)
random variables, then the probability distributions of X1 + X2
+ ... + Xn and are respectively
the N(nμ, nσ2) and N(μ, σ2/n).
These two distributions, in statistical inference point of view, can be
considered respectively as the sampling distributions of the sample total and
sample mean of a random sample drawn from the N(μ, σ2)
distribution. The notation N(μ, σ2) refers to
the normal distribution having mean μ and variance σ2.
Related Topics