Test of Hypotheses for Equality of Means of two Populations (Population Variances are Known)

TEST OF HYPOTHESES FOR EQUALITY OF MEANS OF TWO POPULATIONS (Population variances are known)

Procedure:

Step-1 : Let µ_X and σ_X² be respectively the mean and the variance of Population -1. Also, let µ_Y and σ_Y² be respectively the mean and the variance of Population -2 under study. Here σ_X² and σ_Y² are known admissible values.

Frame the null hypothesis as H₀: µ_X = µ_Y and choose the suitable alternative hypothesis from 

H₁: µ_X ≠ µ_Y (ii) H₁: µ_X> µ_Y (iii) H₁: µ_X< µ_Y

Step-2 : Let (X₁, X₂, …, X_m) be a random sample of m observations drawn from Population-1 and (Y₁, Y₂, …, Y_n) be a random sample of n observations drawn from Population-2, where m and n are large(i.e., m ≥ 30 and n ≥ 30). Further, these two samples are assumed to be independent.

Step-3 : Specify the level of significance, α.

Step-4 : Consider the test statistic 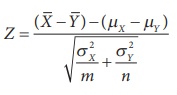 under H₀, where  and  are respectively the means of the two samples described in Step-2.

 The approximate sampling distribution of the test statistic Z = under H₀ (i.e., µ_X = µ_Y) is the N(0,1) distribution.

 It may be noted that the test statistic, when .

Step-5 : Calculate the value of Z for the given samples (x₁, x₂, x₃,…. x_m) and (y₁, y ₂, y ₃,…. y_m) as .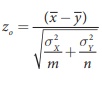

Here,  and  are respectively the values of  and  for the given samples.

Step-6 : Find the critical value, z_e, corresponding to α and H₁ from the following table

Step-7 : Make decision on H₀ choosing the suitable rejection rule from the following table corresponding to H₁. corresponding to H₁.

Example 1.10

Performance of students of X Standard in a national level talent search examination was studied. The scores secured by randomly selected students from two districts, viz., D₁ and D₂ of a State were analyzed. The number of students randomly selected from D₁ and D₂ are respectively 500 and 800. Average scores secured by the students selected from D₁ and D₂ are respectively 58 and 57. Can the samples be regarded as drawn from the identical populations having common standard deviation 2? Test at 5% level of significance.

Solution:

Step 1 : Let μ_X and μ_Y be respectively the mean scores secured in the national level talent search examination by all the students from the districts D ₁ and D₂ considered for the study. It is given that the populations of the scores of the students of these districts have the common standard deviation σ = 2. The null and alternative hypotheses are

Null hypothesis: H₀: µ_X = µ_Y

i.e., average scores secured by the students from the study districts are not significantly different.

Alternative hypothesis: H₁: µ_X ≠ µ_Y

i.e., average scores secured by the students from the study districts are significantly different. It is a two-sided alternative.

Step 2 : Data

The given sample information are

Size of the Sample-1 (m) = 500

Size of the Sample-2 (n) = 800. Hence, both the samples are large.

Mean of Sample-1 (  ) = 58

Mean of Sample-2 (  ) = 57

Step 3 : Level of significance

 α= 5%

Step 4 : Test statistic

The test statistic under the null hypothesis H₀ is

Since both m and n are large, the sampling distribution of Z under H₀ is the N(0, 1) distribution.

Step 5 : Calculation of Test Statistic

The value of Z is calculated for the given sample information from

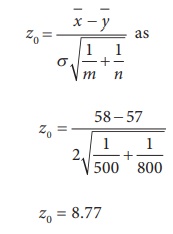
Step-6 : Critical value

Since H₁ is a two-sided alternative hypothesis, the critical value at α = 0.05 is z_e = z_0.025 = 1.96.

Step-7 : Decision

Since H₁ is a two-sided alternative, elements of the critical region are defined by the rejection rule |z₀ | ≥ z _e = z_0.025. For the given sample information, |z₀| = 8.77 > z_e = 1.96. It indicates that the given sample contains sufficient evidence to reject H₀. Thus, it may be decided that H₀ is rejected. Therefore, the average performance of the students in the districts D₁ and D₂ in the national level talent search examination are significantly different. Thus the given samples are not drawn from identical populations.