Level of Significance, Critical Region and Critical Value(S)

LEVEL OF SIGNIFICANCE, CRITICAL REGION AND CRITICAL VALUE(S)

In a given hypotheses testing problem, the maximum probability with which we would be willing to tolerate the occurrence of type I error is called level of significance of the test. This probability is usually denoted by ‘α’. Level of significance is specified before samples are drawn to test the hypothesis.

The level of significance normally chosen in every hypotheses testing problem is 0.05 (5%) or 0.01 (1%). If, for example, the level of significance is chosen as 5%, then it means that among the 100 decisions of rejecting the null hypothesis based on 100 random samples, maximum of 5 of among them would be wrong. It is emphasized that the 100 random samples are drawn under identical and independent conditions. That is, the null hypothesis H₀ is rejected wrongly based on 5% samples when H₀ is actually true. We are about 95% confident that we made the right decision of rejecting H₀.

Critical region in a hypotheses testing problem is a subset of the sample space whose elements lead to rejection of H₀. Hence, its elements have the dimension as that of the sample size, say, n(n > 1). That is,

Critical Region = { x = (x₁ , x₂ , ..., x_n )| H₀ is rejected}

A subset of the sample space whose elements does not lead to rejection of H₀ may be termed as acceptance region, which is the complement of the critical region. Thus,

S = {Critical Region} U {Acceptance Region}.

Test statistic, a function of statistic(s) and the known value(s) of the underlying parameter(s),is used to make decision on H₀. Consider a hypotheses testing problem, which uses a test statistic t ( X) and a constant c for deciding on H₀ . Suppose that H₀ is rejected, when t(x) > c . It is to be noted here that t ( X) is a scalar and is of dimension one. Its sampling distribution is a univariate t (X) satisfying the condition t ( x) > c will identify the probability distribution. The values of samples in the sample space, which lead to rejection of H₀. It does not mean that { t | t(x) > c } is the corresponding critical region. The value ‘c’, distinguishing the elements of the critical region and the acceptance region, is referred to as critical value. There may be one or many critical values for a hypotheses testing problem. The critical values are determined from the sampling distribution of the respective test statistic under H₀.

Example 1.4

Suppose an electrical equipment manufacturing industry receives screws in lots, as raw materials. The production engineer decides to reject a lot when the number of defective screws is one or more in a randomly selected sample of size 2.

Then, X₁ and X₂ are iid random variables and they have the Bernoulli (P) distribution.

Let  H₀ : P = 1/3  and H₁ : P = 2/3

The sample space is S = {(0,0),(0,1),(1,0),(1,1)}

If T(X₁, X₂) represents the number of defective screws, in each random sample, then the statistic T(X₁, X₂) = X₁ + X₂ is a random variable distributed according to the Binomial (2, P) distribution. The possible values of T(X₁, X₂) are 0, 1 and 2. The values of T(X₁, X₂) which lead to rejection of H₀ constitute the set {1,2}.

But, the critical region is defined by the elements of S corresponding to T(X₁,X₂) = 1 or 2.

Thus, the critical region is {(0,1), (1,0), (1,1)} whose dimension is 2.

Note 8: When the sampling distribution is continuous, the set of values of t ( X) corresponding to the rejection rule will be an interval or union of intervals depending on the alternative hypothesis. It is empahazized that these intervals identify the elements of critical region, but they do not constitute the critical region.

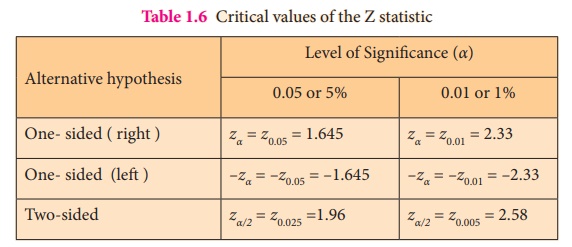
When the sampling distribution of the test statistic Z is a normal distribution, the critical values for testing H₀ against the possible alternative hypothesis at two different levels of significance, say 5% and 1% are displayed in Table 1.6.

Table 1.6 Critical values of the Z statistic