Definition, Example Solved Problems | Statistics - One-Tailed and Two-Tailed Tests | 12th Statistics : Chapter 1 : Tests of Significance - Basic Concepts and Large Sample Tests
Chapter: 12th Statistics : Chapter 1 : Tests of Significance - Basic Concepts and Large Sample Tests
One-Tailed and Two-Tailed Tests
ONE-TAILED AND TWO-TAILED TESTS
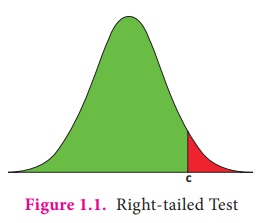
In some hypotheses testing problem, elements of the critical
region may be identified by a rejection rule of the type t ( X) ≥ c. In
this case, P( t ( X) ≥ c) will be the area, which falls at the right end
(Figure1.1) under the curve representing the sampling distribution of t (X).
The statistical test defined by this kind of critical region is called right-tailed test.
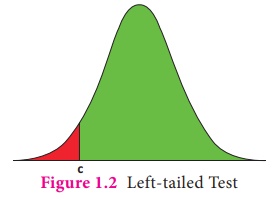
On the other hand, suppose that the rejection rule t (X) ≤
c determines the elements of the critical region. Then, P( t (X) ≤ c)
will be the area, which falls at the left end (Figure.1.2) under the curve
representing the sampling distribution of t (X) . The statistical test
defined by this kind of critical region is called left -tailed test.
The above two tests are commonly known as one-tailed tests.
Note 9: It should be noted that the sampling distribution of t (X) need not be with
symmetric shape always. Sometimes, it may be positively or negatively
skewed.
Example 1.5
Suppose a pizza restaurant claims its average pizza delivery time
is 30 minutes. But you believe that the restaurant takes more than 30 minutes.
Now, the null and the alternate hypotheses can be formulated as
H0 : μ = 30 minutes and H1: μ > 30
minutes
Suppose that the decision is taken based on the delivery times of
4 randomly chosen pizza deliveries of the restaurant. Let X1
, X2, X3, and X4
represent the delivery times of the such four occasions. Also, let H0
be rejected, when the sample mean exceeds 31. Then, the critical region is
Critical
Region = 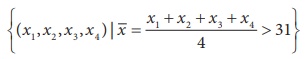
In
this case, P( ![]() > 31) –will
be the area, which fall at the right end under the curve representing the
sampling distribution of
> 31) –will
be the area, which fall at the right end under the curve representing the
sampling distribution of ![]() . Hence, this test can be categorized
as a right-tailed test.
. Hence, this test can be categorized
as a right-tailed test.
Suppose
that H0 is rejected, when either t(X) ≤ a or t(X)
≥ b) holds. In this case, P(t (X) ≤ a)
and P(t (X) ≥ b) will be the areas, which fall
respectively at left and right ends under the curve representing the sampling
distribution of t ( X) (Figure
1.3). The statistical test defined with
this kind of rejection rule is known as two-tailed
test.
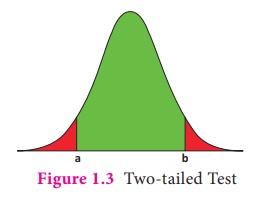
Figure 1.3 Two-tailed Test
Example 1.6
A manufacturer of ball-bearings, which are used in some machines,
inspects to see whether the diameter of each ball-bearing is 5 mm. If the
average diameter of ball-bearings is less than 4.75 mm or greater than 5.10 mm,
then such ball-bearings will cause damages to the machine.
Here the null and the alternate hypotheses are
H0 : μ = 5 and H1: μ ≠ 5.
Suppose that the decision on H0 is made based on
the diameter of 10 randomly selected ball-bearings. Let Xi, i
= 1, 2, …, 10 represent the diameter of the randomly chosen ball bearings.
Then, the critical region is
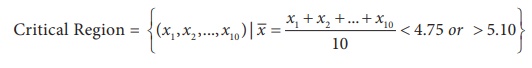
In this case, P (![]() <4.75) is the area, which will fall at the left end and P(
<4.75) is the area, which will fall at the left end and P(![]() > 5.10) is the
area, which will fall at the right end under the curve representing the
sampling distribution of
> 5.10) is the
area, which will fall at the right end under the curve representing the
sampling distribution of ![]() . This kind of test can be categorized
as a two-tailed test (see Figure 1.3).
. This kind of test can be categorized
as a two-tailed test (see Figure 1.3).
Related Topics