Summary - Applications of Differentiation

SUMMARY

Demand is the relationship between the quantity demanded and the price of a commodity.

Supply is the relationship between the quantity supplied and the price of a commodity.

Cost is the amount spent on the production of a commodity.

Revenue is the amount realised by selling the output produced on commodity.

Profit is the excess of total revenue over the cost of production.

Elasticity of a function y = f(x) at a point x is the limiting case of ratio of the relative change in y to the relative change in x

Equilibrium price is the price at which the demand of a commodity is equal to its supply.

Marginal cost is interpreted as the approximate change in production cost of ( x + 1)^th unit, when the production level is x units.

Marginal Revenue is interpreted as the approximate change in revenue made on by selling of ( x + 1)^th unit, when the sale level is x units.

A function f(x) is said to be increasing function in the interval [a, b] if x₁ < x₂ ⟹ f (x₁ ) =< f (x₂) for all x₁, x₂ â²ˆ  [a,b]

A function f(x) is said to be strictly increasing in [a, b] if x1 < x2 âŸ¹ f (x1 ) < f (x2) for all x1, x2 â²ˆ  [a,b]

A function f(x) is said to be decreasing function in [a,b] if x1 < x2 âŸ¹ f (x1 ) >= f (x2) for all x1, x2 â²ˆ  [a,b]

A function f(x) is said to be strictly decreasing function in [a, b] if x1 < x2 âŸ¹ f (x1 ) > f (x2) for all x1, x2 â²ˆ  [a,b]

Let f be a differentiable function on an open interval (a,b) containing c and suppose that f'’(c) exists.

(i) If f '(c) = 0 and f "(c) > 0, then f has a local minimum at c.

(ii) If f '(c) = 0 and f "(c) < 0,then f has a local maximum at c.

A function f(x,y) of two independent variables x and y is said to be homogeneous in x and y of degree n if for t > 0  f (tx , ty ) = t ⁿ f ( x, y)

If u = f ( x , y) is a homogeneous function of degree n, then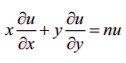 

The partial elasticity of demand  q with respect to p₁ is defined to be

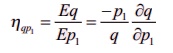
The partial elasticity of demand q with respect to p₂ is defined to be