Applications of Differentiation - Successive partial derivatives | 11th Business Mathematics and Statistics(EMS) : Chapter 6 : Applications of Differentiation
Chapter: 11th Business Mathematics and Statistics(EMS) : Chapter 6 : Applications of Differentiation
Successive partial derivatives
Successive partial derivatives
Consider the functionu u = f( x,
y) . From this we can find 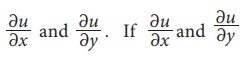 are functions of x and y, then
they may be differentiated partially again with respect to either of the independent variables, (x or y) denoted by
are functions of x and y, then
they may be differentiated partially again with respect to either of the independent variables, (x or y) denoted by  .
.
These derivatives are called
second order partial derivatives. Similarly, we can find the third order
partial derivatives, fourth order partial derivatives etc., if they exist. The
process of finding such partial derivatives are called successive partial derivatives.
If we differentiate u = f(x,y) partially with respect to x and again differentiating partially with respect to y, we obtain 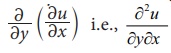 .
.
Similarly, if we differentiate u = f(x,y)
partially with respect to y
and again differentiating partially with respect to x, 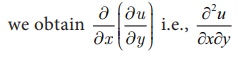
NOTE
If u(x,y)is
a continuous function of x and y then
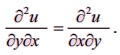
Homogeneous functions
A function f(x,y) of two independent
variables x and y is said to be homogeneous in x
and y of degree n if f
(tx , ty ) = t n
f ( x, y) for t > 0.
Related Topics