Applications of differentiation in business and economics - Elasticity | 11th Business Mathematics and Statistics(EMS) : Chapter 6 : Applications of Differentiation
Chapter: 11th Business Mathematics and Statistics(EMS) : Chapter 6 : Applications of Differentiation
Elasticity
Elasticity
Elasticity ãöñã of the function y = f (x ) at a
point x is defined as the limiting
case of ratio of the relative change in y
to the relative change in x.
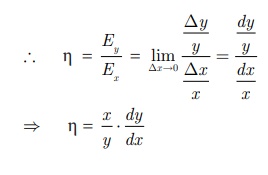
(i) Price elasticity of demand
Price elasticity of demand is the
degree of responsiveness of quantity demanded to a change in price.
If x is demand and p is unit
price of the demand function x = f(p),
then the elasticity of demand with respect to the price is defined as hd =
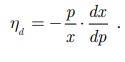
(ii) Price elasticity of supply :
Price elasticity of supply is the
degree of responsiveness of quantity supplied to a change in price.
If x is supply and p is unit price of the supply function x = g(p), then the elasticity of supply with respect to the price is defined as hs
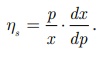
Some important results on price elasticity
(i) If |
öñ |>1, then the quantity demand or supply is said to be elastic.
(ii) If |
öñ |=1, then the quantity demand or supply is said to be unit elastic.
(iii) If | öñ |<1, then the
quantity demand or supply is said to be inelastic.
Remarks:
(i) Elastic : A quantity demand
or supply is elastic when its quantity responds greatly to changes in its
price.
Example: Consumption of onion and
its price.
(ii) Inelastic : A quantity
demand or supply is inelastic when its quantity responds very little to changes
in its price.
Example: Consumption of rice and its price.
(iii) Unit elastic : A quantity
demand or supply is unit elastic when its quantity responds as the same ratio
as changes in its price.
Relationship among Marginal revenue [MR], Average revenue [AR] and Elasticity of demand[öñd].
We know that R(x)=px
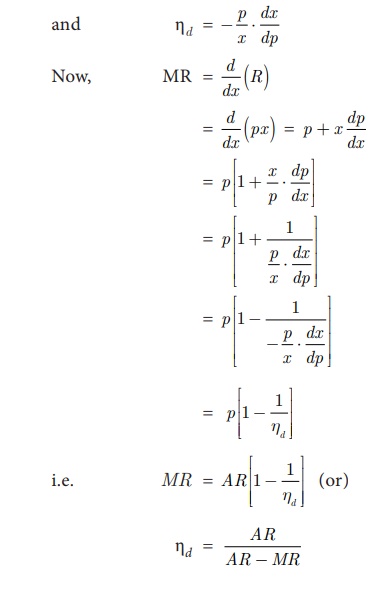
Example 6.1
The total cost function for the
production of x units of an item is
given by

(i) Average cost
(ii) Average variable cost
(iii) Average fixed cost
(iv) Marginal cost and
(v) Marginal Average cost
Solution:
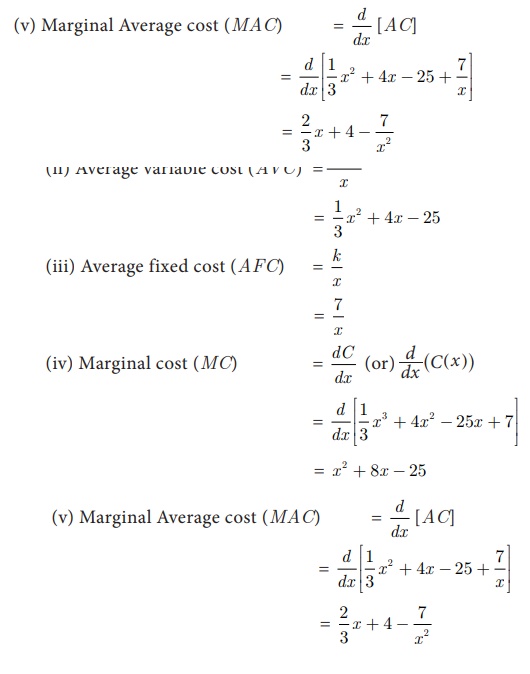
Example 6.2
The total cost C in Rupees of making x units of product is C (x ) = 50 + 4x + 3ãx . Find
the marginal cost of the product at 9 units of output.
Solution:
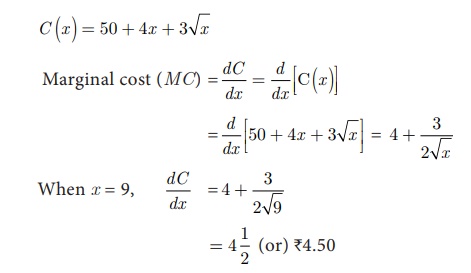
MC is ã¿ 4.50 , when the level of output is 9 units.
Example 6.3
Find the equilibrium price and
equilibrium quantity for the following demand and supply functions.
Demand : x = 1/2 (5 ã p) and
Supply : x = 2pã3
Solution:

Example 6.4
For the demand function x=20/P+1, find the elasticity of demand
with respect to price at a point p =
3. Examine whether the demand is elastic at p
= 3.
Solution:

Example 6.5
Find the elasticity of supply for
the supply function x = 2p2 - 5 p + 1
Solution:

Example 6.6

Example 6.7
A demand function is given by xpn = k where n and k are constants. Prove that elasticity
of demand is always constant.
Solution:
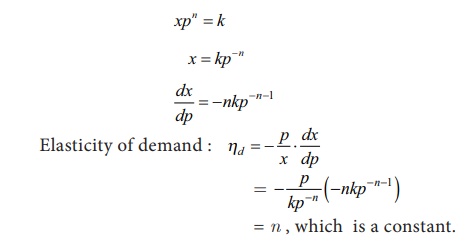
Example 6.8
For the given demand function p = 40ãx, find the value of the output when öñd =1
Solution:

Example 6.9
Find the elasticity of demand in
terms of x for the demand law p = (a-bx)1/2 . Also find the
values of x when elasticity of demand
is unity.
Solution:

Example 6.10
Verify the relationship of
elasticity of demand, average revenue and marginal revenue for the demand law p = 50 - 3x .
Solution:

Example 6.11
Find the elasticity of supply for
the supply law x = p / p+5 when p = 20
and interpret your result.
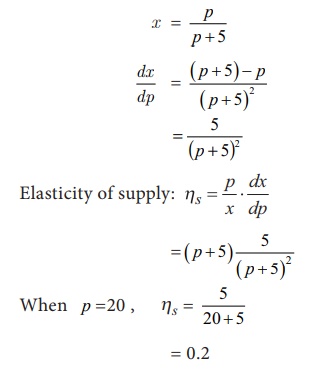
Interpretation:
ôñ
z If the price increases by 1% from p = ã¿ 20, then
the quantity of supply increases by 0.2% approximately.
ôñ
z If the price decreases by 1% from p = ã¿ 20, then
the quantity of supply decreases by 0.2% approximately.
Example 6.12
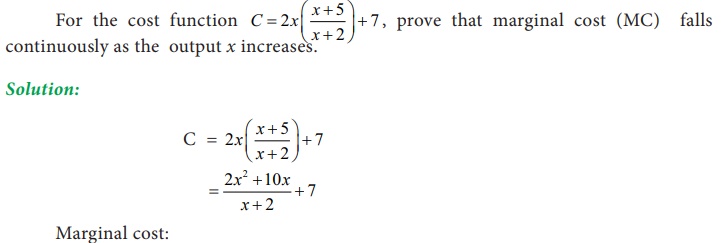
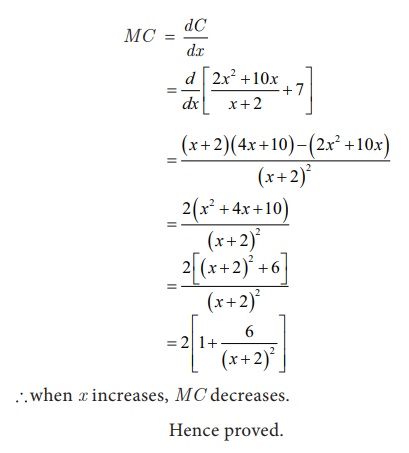
Example 6.13
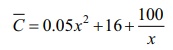 is the manufacturerãs average cost function. What is the marginal cost when 50 units are produced and interpret your result.
is the manufacturerãs average cost function. What is the marginal cost when 50 units are produced and interpret your result.
Solution:
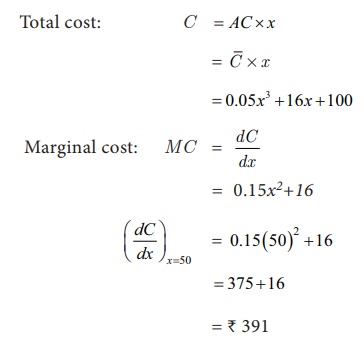
Interpretation:
If the production level is
increased by one unit from x = 50,
then the cost of additional unit is approximately equal to ã¿ 391.
Example 6.14
For the function y x3+19,
find the values of x when its
marginal value is equal to 27.
Solution:
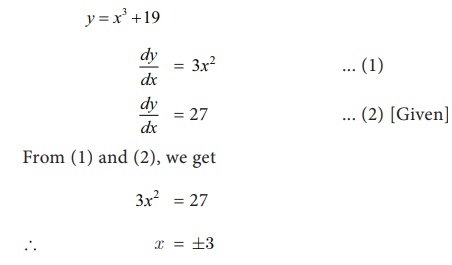
Example 6.15
The demand function for a
commodity is p = 4/x,where
p is unit price. Find the
instantaneous rate of change of demand with respect to price at p=4. Also interpret your result.
Solution:
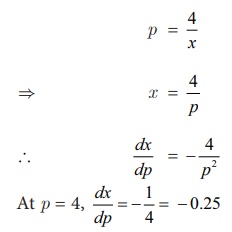
Rate of change of demand with
respect to the price at p
= ã¿ 4 is ã 0.25
Interpretation:
When the price increases by 1%
from the level of p = ã¿ 4, the demand decreases (falls)
by 0.25%
Example 6.16
The demand and the cost function
of a firm are p = 497-0.2x and C = 25x+10000
respectively. Find the output level and price at which the profit is maximum.
Solution:
We know that profit is maximum
when marginal revenue [MR] = marginal cost [MC].
Revenue: R = px

Example 6.17
The cost function of a firm is C = 1/3 x3 ã 3x2 + 9x . Find the level of output (x>0)
when average cost is minimum.
Solution:
We know that average cost [AC] is
minimum when average cost [AC] = marginal cost [MC].
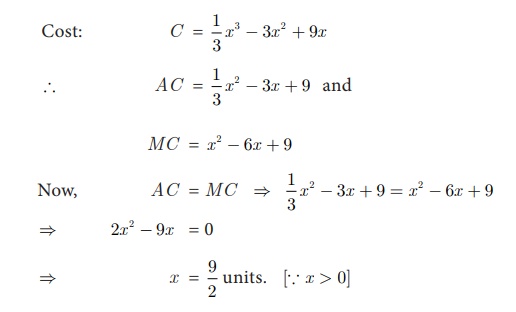


Related Topics