Partial Derivatives

Partial Derivatives

Partial derivative of a function of several variables is its derivative with respect to one of those variables, keeping other variables as constant. In this section, we will restrict our study to functions of two variables and their derivatives only.

Let u = f ( x , y)  be a function of two independent variables x and y.

The derivative of u with respect to x when x varies and y remains constant is called the partial derivative of u with respect to x, denoted by

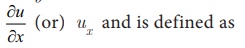
provided the limit exists. Here ∆x is a small change in x

The derivative of u with respect to y, when y varies and x remains constant is called the partial derivative of u with respect to y, denoted by

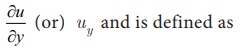
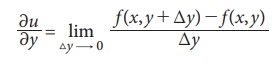
provided the limit exists. Here ∆y is a small change in y.

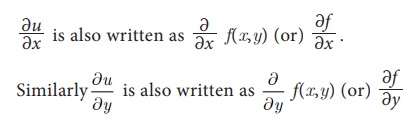
The process of finding a partial derivative is called partial differentiation.