Maxima and minima - Applications of Differentiation - Stationary Value of a function | 11th Business Mathematics and Statistics(EMS) : Chapter 6 : Applications of Differentiation
Chapter: 11th Business Mathematics and Statistics(EMS) : Chapter 6 : Applications of Differentiation
Stationary Value of a function
Stationary Value of a function
Let f(x) be a continuous
function on [a, b] and differentiable in (a,
b). f(x) is said to be
stationary at x = a if f
' (a)=0.
The stationary value of f(x)
is f(a) . The point (a,f(a)
) is called stationary point.
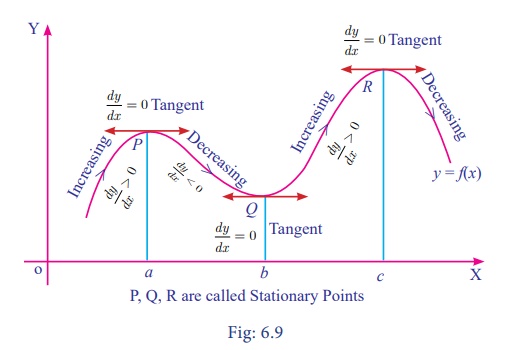
In figure 6.9 the function y = f(x) has stationary at x = a,x = b
and x = c.
At these points, dx/dy = 0 . The
tangents at these points are parallel to x
– axis.
NOTE
By drawing the
graph of any function related to economics data, we can study the trend of the
business related to the function and therefore, we can predict or forecast the
business trend.
Example 6.18
Show that the function f(x)
= x3 − 3x2 + 4x , x ∈ R is
strictly increasing function on R.
Solution :
f(x) =
x 3 − 3x 2 + 4x ,
x ∈ R
f'(x) = 3x2–6x+4
= 3x2–6x+3+1
= 3(x–1)2+1
> 0, for all x∈R
Therefore, the function f is strictly increasing on (-∞,∞).
Example 6.19
Find the interval in which the
function f(x)=x2–4x+6 is strictly increasing and strictly
decreasing.
Solution :
Given
that f(x) =x2–4x+6
Differentiate with respect to x,
f' (x) = 2x–4
When f’ (x) = 0 → 2x–4=0
x = 2.
Then the real line is divided
into two intervals namely (–∞,2) and (2,∞)
[ To choose the sign of f ’(x) choose any values for x from the intervals ans substitute in f ‘ (x) and get the sign.]
Example 6.20
Find the intervals in which the
function f given by f(x)=4x3–6x2–72x+30 is
increasing or decreasing.
Solution :
f(x) = 4x3–6x2–72x+30
f ‘(x) = 12x2–12x–72
= 12(x2–x–6)
= 12(x–3)(x+2)
f ‘ (x) = 0 ⟹ 12(x–3)(x+2)=0
x= 3 (or) x = –2
f(x) has stationary at x =3 and at x = –2.
These points divides the whole
interval into three intervals namely (–∞,–2),(–2,3) and (3,∞).
Example 6.21
Find the stationary value and the
stationary points f(x)=x2+2x–5.
Solution :
Given that f(x) = x2
+ 2x – 5 … (1)
f'(x) = 2x + 2
At stationary points, f ‘(x) = 0
⟹ 2x + 2 = 0
⟹
x = –1
f(x) has stationary value at x = –1
When x = –1, from (1)
f(–1) =
(–1)2+2(–1)–5
= – 6
Stationary value of f (x)
is – 6
Hence stationary point is (–1,–6)
Example 6.22
Find the stationary values and
stationary points for the function
f(x)=2x3+9x2+12x+1.
Solution :
Given that f(x) = 2x3+9x2+12x+1.
f'(x) = 6x2+18x+12
= 6(x2+3x+2)
= 6(x+2)(x+1)
f'(x) = 0 ⟹ 6 (x+2)(x+1) = 0
x + 2 = 0 (or) x + 1 = 0.
x = –2 (or) x = –1
f(x) has stationary points at x = – 2 and x = – 1
Stationary values are obtained by
putting x = – 2 and x = – 1
When x = – 2
f(–2) =
2(–8)+9(4)+12(–2)+1
= –3
When x = – 1
f(–1) =
2(–1)+9(1)+12(–1)+1
= –4
The stationary points are (–2,–3)
and (–1,–4)
Example 6.23
The profit function of a firm in
producing x units of a product is
given by P(x)= x3/3 + x2 + x. Check whether the firm is running a profitable business or not.
Solution :
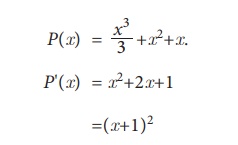
It is clear that P'(x)>0
for all x.
The firm is running a profitable
business.
IMPORTANT NOTE
Let R(x) and C(x)
are revenue function and cost function respectively when x units of commodity is produced. If R(x) and C(x)
are differentiable for all x > 0
then P(x) = R(x) – C(x) is maximized when Marginal Revenue = Marginal cost. That is, when Rl (x)= C’ (x) profit is maximum at
its stationary point.
Example 6.24
Given C(x)= x2/6 +5x+200 and p(x)
= 40–x are the cost price and selling
price when x units of commodity are
produced. Find the level of the production that maximize the profit.
Solution :
Related Topics