Problems on profit maximization and minimization of cost function

Problems on profit maximization and minimization of cost function:

Example 6.27

For a particular process, the cost function is given by C = 56 - 8x + x² , where C is cost per unit and x, the number of unit’s produced. Find the minimum value of the cost and the corresponding number of units to be produced.

Solution :

C = 56 - 8x + x²

Differentiate with respect to x,

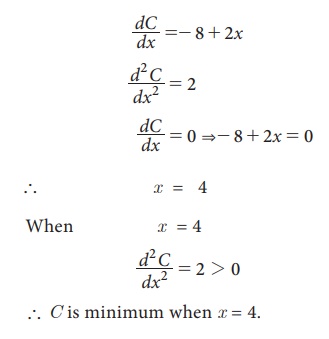
The minimum value of cost = 56–32+16

= 40

The corresponding number of units produced = 4

Example 6.28

The total cost function of a firm is C(x) = x³/3 – 5x² + 28x + 10 where x is the output. A tax at the rate of ₹ 2 per unit of output is imposed and the producer adds it to his cost. If the market demand function is given by p = 2530 – 5x, where p is the price per unit of output, find the profit maximizing the output and price.

Solution :

Total revenue:  R = p x

= (2530 – 5x)x

= 2530x–5x²

Tax at the rate ₹ 2 per x unit = 2x.

= 2530 – 5(50)

= ₹ 2280.

Example 6.29

The manufacturing cost of an item consists of ₹ 1,600 as over head material cost ₹ 30 per item and the labour cost ₹ a (x² /100) for x items produced. Find how many items be produced to have the minimum average cost.

Solution :

As per given information for producing x units of certain item C(x) = labour cost + material cost + overhead cost

AC is minimum at x = 400

Hence 400 items should be produced for minimum average cost.