Applications of partial derivatives - Production function and marginal productivities of two variables | 11th Business Mathematics and Statistics(EMS) : Chapter 6 : Applications of Differentiation
Chapter: 11th Business Mathematics and Statistics(EMS) : Chapter 6 : Applications of Differentiation
Production function and marginal productivities of two variables
Applications of partial derivatives
In this section we solve problems
on partial derivatives which have direct impact on Industrial areas.
Production function and marginal
productivities of two variables
(i) Production function:
Production P of a firm depends upon several economic factors like capital (K), labour (L), raw materials (R),machinery
(M) etcãÎ Thus P = f(K,L,R,M,ãÎ) is known as production
function. If P depends only on labour
(L) and capital (K), then we write P=f(L,K).
(ii) Marginal productivities:
Let P = f(L,K) be a production function. Then ãP/ãL is called the Marginal productivity of labour and ãP/ãL is called the Marginal productivity of capital.
Eulerãs theorem for homogeneous
production function P(L,K) of degree 1 states that
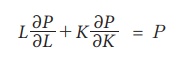
Related Topics