Partial elasticity of demand

Partial elasticity of demand

Let q = f( p₁, p₂) be the demand for commodity A, which depends upon the prices

p₁ and p₂ of commodities A and B respectively.

The partial elasticity of demand q with respect to p₁ is defined to be

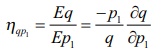
The partial elasticity of demand q with respect to p₂ is defined to be

Example 6.40

Find the marginal productivities of capital (K) and labour (L) if

=10L + 0.1L² + 5K - 0.3K² + 4KL when K=L=10.

Solution:

We have P = 10L + 0.1L² + 5K - 0.3K² + 4KL

Example 6.41

The production function for a commodity is P=10L + 0.1L² + 15K - 0.2K² + 2KL where L is labour and K is Capital.

(i) Calculate the marginal products of two inputs when 10 units of each of labour and Capital are used

(ii) If 10 units of capital are used, what is the upper limit for use of labour which a rational producer will never exceed?

Solution:

(i) Given the production is P = 10L − 0 . 1L² +15K − 0 .2K² + 2KL

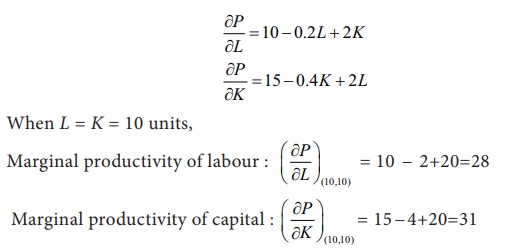
(ii)  Upper limit for use of labour when K=10 is given by a ²₂^P_L k ≥0

10 − 0.2L+20 ≥0

30 ≥ 0.2L

i.e.,L ≤ 150

Hence the upper limit for the use of labour will be 150 units

Example 6.42

Exercise 6.5