Maxima and minima - Applications of Differentiation - Increasing and decreasing functions | 11th Business Mathematics and Statistics(EMS) : Chapter 6 : Applications of Differentiation
Chapter: 11th Business Mathematics and Statistics(EMS) : Chapter 6 : Applications of Differentiation
Increasing and decreasing functions
Increasing and decreasing functions
Before learning the concept of
maxima and minima, we will study the nature of the curve of a given function
using derivative.
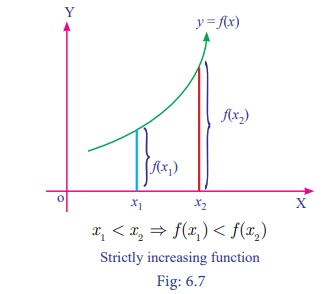
(i) Increasing function
A function f(x) is said to be
increasing function in the interval [a,b] if
x1 < x2 ã f
(x 1 )ãÊ f (x 2 ) for all x 1 , x2 ã |a , ]
A function f(x) is said to be
strictly increasing in [a,b] if
x1 < x2 ã f
(x 1 )< f (x 2 ) for all x 1 , x2 ã [a ,b]
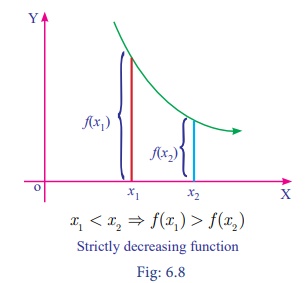
(ii) Decreasing function
A function f(x) is said to be
decreasing function in [a, b] if
x1 < x2 ã f
(x 1 )ãË f (x 2 ) for all x 1 , x2 ã [a ,b]
A function f(x) is said to be
strictly decreasing function in [a,b] if x
x1 < x2 ã f (x 1 )> f (x 2 ) for all x 1 , x2 ã [a ,b]
NOTE
A function is said
to be monotonic function if it is either an increasing function or a decreasing
function.
Derivative test for increasing and decreasing function
Theorem:6.1 (Without Proof)
Let f(x) be a continuous
function on [a,b] and differentiable on the open interval (a,b), then
(i) f(x)
is increasing in [a, b] if f ãý (x ) ãË 0
(ii) f(x) is decreasing in [a,
b] if f ãý (x ) ãÊ 0
Remarks:
(i) f(x)
is strictly increasing in (a,b) if
f ãý (x ) > 0 for every x ã (a ,b)
(ii) f(x)
is strictly decreasing in (a,b) if
f ãý (x ) < 0 for every x ã (a ,b)
(iii) f(x) is said to be a constant
function if f ãý (x ) = 0
Related Topics