Solubility Product

Solubility Product

We have come across many precipitation reactions in inorganic qualitative analysis. For example, dil HCl is used to precipitate Pb²⁺ ions as PbCl₂ which is sparingly soluble in water. Kidney stones are developed over a period of time due to the precipitation of Ca²⁺ (as calcium oxalate etc…). To understand the precipitation, let us consider the solubility equilibria that exist between the undissociated sparingly soluble salt and its constituent ions in solution.

For a general salt X _m Y_n ,

The equilibrium constant for the above is

K = { [Xⁿ⁺ ]^m [Y^m- ]ⁿ } / { [X_m Y_m ] }

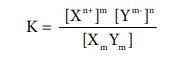
In solubility equilibria, the equilibrium constant is referred as solubility product constant (or) Solubility product.

In such heterogeneous equilibria, the concentration of the solid is a constant and is omitted in the above expression

K_sp = [Xⁿ⁺ ]^m [Y^m- ]ⁿ

The solubility product of a compound is defined as the product of the molar concentration of the constituent ions, each raised to the power of its stoichiometric co – efficient in a balanced equilibrium equation.

Solubility product finds useful to decide whether an ionic compound gets precipitated when solution that contains the constituent ions are mixed.

When the product of molar concentration of the constituent ions i.e., ionic product, exceeds the solubility product then the compound gets precipitated.

The expression for the solubility product and the ionic product appears to be the same but in the solubility product expression, the molar concentration represents the equilibrium concentration and in ionic product, the initial concentration (or) concentration at a given time ‘t’ is used.

In general we can summarise as,

Ionic product > K_sp , precipitation will occur and the solution is super saturated.

Ionic product < K_sp , no precipitation and the solution is unsaturated.

Ionic product = K_sp , equilibrium exist and the solution is saturated.

Example 8.9

Indicate find out whether lead chloride gets precipitated or not when 1 mL of 0.1M lead nitrate and 0.5 mL of 0.2 M NaCl solution are mixed? K_sp of PbCl₂ is 1.2 × 10^-5.

Ionic product = (6.7 × 10^-2 )(6.7 ×10⁻² )² = 3.01 × 10^-4

Since, the ionic product 3.01 × 10^-4 is greater than the solubility product (1.2 × 10^-5 ) , PbCl₂ will get precipitated.

Determination of solubility product from molar solubility

Solubility product can be calculated from the molar solubility i.e., the maximum number of moles of solute that can be dissolved in one litre of the solution.

For a solute X_m Y_n ,

X_m Y_n (s) ↔ mXⁿ⁺ (aq) + nY^m-(aq)

From the above stoichiometrically balanced equation we have come to know that 1 mole of X_m Y_n (s) dissociated to furnish ‘m’ moles of Xⁿ⁺ and ‘n’ moles of Y^m- if ‘s’ is molar solubility of X_m Y_n , then

[Xⁿ⁺] = ms and [ Y^m- ]=ns

∴K_sp = [Xⁿ⁺]^m [Y^m-]ⁿ

K_sp = (ms)^m (ns)ⁿ

K_sp =(m)^m (n)ⁿ (s)^m+n

Example 8.10

Establish a relationship between the solubility product and molar solubility for the Following

a. BaSO₄

b.Ag₂ (CrO₄ )

 BaSO₄ (s) ←^H₂^O→ Ba²⁺ (aq) + SO₄^2-(aq)

K_sp =[Ba²⁺ ][SO₄^2-]

= (s) (s)

K_sp = S²

Ag₂ CrO₄ (s) ←^H2O→ 2Ag ⁺ (aq) + CrO₄^2-(aq)

K_sp = [Ag⁺ ]²[CrO₄^2-]

= (2s)² (s)

K_sp =4s³