Ionic Equilibrium | Chemistry - Numerical Problems with Answers, Solution | 12th Chemistry : UNIT 8 : Ionic Equilibrium
Chapter: 12th Chemistry : UNIT 8 : Ionic Equilibrium
Numerical Problems with Answers, Solution
Example 8.1
Calculate the concentration of OH- in a fruit juice which contains 2 ├Ś10-3 M, H3O+ ion. Identify the nature of the solution.
Given that H3O+ = 2 ├Ś10-3 M
Kw = [H3O+ ][OH - ]
Ōł┤[OH - ]= Kw /[H3O+ ] = [1 ├Ś├Ś10-14] / [2 x 10 3] =5 ├Ś10-12 M
2 ├Ś10-3 >> 5 ├Ś10-12
i.e., [H3O+ ] >> [OH-], hence the juice is acidic in nature
Example 8.2
Calculate the pH of 0.001M HCl solution
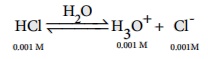
H3O+ from the auto ionisation of H2O (10-7M) is negligible when compared to the H3O+ from 10-3M HCl.
Hence [H3O+ ]= 0.001 mol dmŌĆō3
pH = -log10 [H3O+]
= -log10 (0.001)
= -log10 (10-3 ) = 3
Note: If the concentration of the acid or base is less than 10ŌĆō6 M, the concentration of H3O+ produced due to the auto ionisation of water cannot be negleted and in such cases
[H3O+] = 10-7(from water) + [H3O+] (from the acid)
similarly, [OH-] = 10-7 M (from water) + [OH-] (from the base)
Example 8.3
Calculate pH of 10-7 M HCl
If we do not consider [H3O+ ] from the ionisation of H2O,
then [H3O+ ] = [HCl] = 10-7M
i.e., pH = 7, which is a pH of a neutral solution. We know that HCl solution is acidic whatever may be the concentration of HCl i.e, the pH value should be less than 7. In this case the concentration of the acid is very low (10-7M) Hence, the H3O+ (10-7M) formed due to the auto ionisation of water cannot be neglected.
so, in this case we should consider [H3O+ ] from ionisation of H 2O
[H3O+ ] = 10-7 (from HCl) + 10-7 (from water)
= 10-7 (1+1)
= 2 ├Ś10-7
pH = -log10[H3O+ ]
= - log 2 - (-7).log10 10
= 7-log 2
= 7-0.3010 = 6.6990
= 6.70
Example 8.4
A solution of 0.10M of a weak electrolyte is found to be dissociated to the extent of 1.20% at 25oC . Find the dissociation constant of the acid.
Given that ╬▒=1.20%=1.20/100
= 1.2 ├Ś 10-2
Ka = ╬▒2c
= (1.2 ├Ś 10-2 )2 (0.1) = 1.44 ├Ś10-4 ├Ś10-1
= 1.44 ├Ś 10-5
Example 8.5
Calculate the pH of 0.1M CH3COOH solution. Dissociation constant of acetic acid is 1.8 ├Ś10-5 .
pH=-log[H+ ]
For weak acids,
[H+ ]= ŌłÜ [Ka ├Ś C]
= ŌłÜ (1.8 ├Ś10-5 ├Ś 0.1)
=1.34 ├Ś10-3M pH=-log (1.34 ├Ś10-3)
= 3 - log1.34
= 3 - 0.1271
= 2.8729 Ōēł2.87
Example 8.6
Find the pH of a buffer solution containing 0.20 mole per litre sodium acetate and 0.18 mole per litre acetic acid. Ka for acetic acid is 1.8 ├Ś 10-5 .
pH = pKa + log {[salt]/[acid]}
Given that Ka = 1.8 ├Ś 10-5
Ōł┤ pKa = ŌłÆlog(1.8 ├Ś10ŌłÆ5 ) = 5 ŌłÆlog1.8
= 5 -0.26
= 4.74
Ōł┤pH = 4.74 + log (0.20/0.18)
= 4.74 + log (10/9) = 4.74 + log 10 - log 9
= 4.74 + 1 - 0.95 = 5.74 - 0.95
= 4.79
Example 8.7
What is the pH of an aqueous solution obtained by mixing 6 gram of acetic acid and 8.2 gram of sodium acetate making the volume equal to 500 ml. (Given: Ka for acetic acid is 1.8 ├Ś 10-5 )
According to Henderson ŌĆō Hasselbalch equation,
pH = pKa + log {[salt]/[acid]}
PKa =-logKa =-log(1.8 ├Ś10-5 )= 4.74 (Refer previous example)
Salt = Number of moles of sodium acetate / Volume of the solution ( litre )
Number of moles of sodium acetate = mass of sodium acetate / molar mass of sodium acetate

pH = 4.74 + log 1
pH = 4.74 + 0 = 4.74
Example 8.8
Calculate i) degree of hydrolysis, ii) the hydrolysis constant and iii) pH of 0.1M CH3COONa solution ( pKa for CH3COOH is 4.74).
Solution (a) CH3COONa is a salt of weak acid (CH 3COOH) and a strong base (NaOH).
Hence, the solutions is alkaline due to hydrolysis.
CH3COO - (aq) + H2O(aq) Ōåö CH3COOH (aq) + OH-(aq)
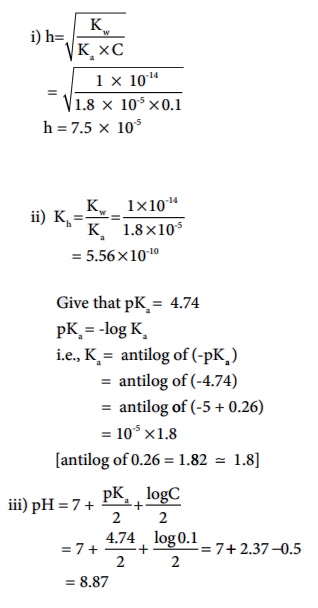
Example 8.9
Indicate find out whether lead chloride gets precipitated or not when 1 mL of 0.1M lead nitrate and 0.5 mL of 0.2 M NaCl solution are mixed? Ksp of PbCl2 is 1.2 ├Ś 10-5.

Ionic product = (6.7 ├Ś 10-2 )(6.7 ├Ś10ŌłÆ2 )2 = 3.01 ├Ś 10-4
Since, the ionic product 3.01 ├Ś 10-4 is greater than the solubility product (1.2 ├Ś 10-5 ) , PbCl2 will get precipitated.
Example 8.10
Establish a relationship between the solubility product and molar solubility for the Following
a. BaSO4
b.Ag2 (CrO4 )
BaSO4 (s) ŌåÉH2OŌåÆ Ba2+ (aq) + SO42-(aq)
Ksp =[Ba2+ ][SO42-]
= (s) (s)
Ksp = S2
Ag2 CrO4 (s) ŌåÉH2OŌåÆ 2Ag + (aq) + CrO42-(aq)
Ksp = [Ag+ ]2[CrO42-]
= (2s)2 (s)
Ksp =4s3
Book Back Questions:
8. Calculate the pH of 0.04 M HNO3 Solution.
Solution:
Concentration of HNO3 = 0.04M
[H3O +] = 0.04 mol dm-3
pH = -log[H3O+]
= -log(0.04)
= -log(4 ├Ś10-2 )
= 2-log4
=2-0.6021
=1.3979 = 1.40
14. Calculate the pH of 1.5├Ś10-3M solution of Ba (OH)2
Answer:
Ba(OH)2 ŌåÆ Ba2+ + 2OH-
1.5 ├Ś10-3M
2 ├Ś1.5 ├Ś 10-3M.
[OH-] = 3 ├Ś10-3M
[ pH+pOH=14]
pH= 14-pOH
pH= 14- ( ŌłÆlog [OH- ] )
= 14+ log [OH- ]
=14+log(3 ├Ś10-3 )
= 14 + log 3 + log 10-3
= 14 + 0.4771ŌłÆ3
= 11+0.4771
pH=11.48
15. 50ml of 0.05M HNO3 is added to 50ml of 0.025M KOH . Calculate the pH of the resultant solution.
Answer:
Number of moles of HNO3 = 0.05 ├Ś 50 ├Ś 10-3
= 2.5 ├Ś 10-3
Number of moles of KOH = 0.025 ├Ś 50 ├Ś 10ŌłÆ3
= 1.25 ├Ś 10-3
Number of moles of HNO3 after mixing
= 2.5 ├Ś 10-3ŌĆō 1.5 ├Ś 10-3
= 1.25 ├Ś 10-3
Ōł┤ concentration of HNO3 = Number of moles of HNO3 / Volume is litre
After mixing, total volume = 100 ml = 100├Ś10-3L
Ōł┤[H + ]= 1.25 ├Ś10-3 moles / 100 ├Ś10-3L
= 1.25 ├Ś10-2 moles L-1
pH = - log [H+ ]
pH = ŌłÆ log(1.25 ├Ś10ŌłÆ2 )
= 2 ŌłÆ 0.0969
= 1.9031
16. The Ka value for HCN is 10-9 . What is the pH of 0.4M HCN solution?
Answer:
Given
Ka =10-9
c=0.4M
pH=-log[H+ ]
[H+ ] = ŌłÜ (Ka ├Ś c.)
= ŌłÜ(10-9 ├Ś0.4)
= 2 ├Ś10-5
Ōł┤pH = - log (2 ├Ś10-5 )
=5-log2
= 5-0.3010
=4.699.
17. Calculate the extent of hydrolysis and the pH of 0.1 M ammonium acetate Given that Ka =Kb =1.8 ├Ś10-5
Answer:
h = ŌłÜKh = ŌłÜ [Kw / KaKb]
= ŌłÜ { 1├Ś10ŌłÆ14 / 1.8├Ś10ŌłÆ5 ├Ś 1.8 ├Ś10ŌłÆ5 }
= ŌłÜ {1/1.8 ├Ś10ŌłÆ4}
= 0.7453 ├Ś10ŌłÆ2
pH = 1/2 pKw + 1/2 pKa - 1/2 pKb
Given that Ka = Kb = 1.8 ├Ś 10-5
if Ka = Kb , then, pKa = pKb
Ōł┤ pH = 1/2 pKw = 1/2 (14) = 7
19. Solubility product of Ag2CrO4 is 1 ├Ś10-12 . What is the solubility of Ag2 CrO4 in 0.01M AgNO3 solution?
Answer:
Given that Ksp =1 ├Ś 10-12
Ag2 CrO4 (s) Ōåö 2 Ag+(aq) + CrO4ŌłÆ2 (aq)
s Ōåö 2s + s
AgNO3 (s) Ōåö Ag+(aq) + NO3- (aq)
0.01M Ōåö 0.01M + 0.01M
[Ag+] = 2s + 0.01
0.01>>2S
Ōł┤ [Ag+ ]= 0.01M
[CrO42ŌłÆ]= s
Ksp = [Ag+]2 [CrO42- ]
1 ├Ś 10-12 = (0.01)2 (s)
(s) = 1 ├Ś 10-12 / (10-2)2 = 1 ├Ś 10ŌłÆ8 M
20. Write the expression for the solubility product of Ca3 (PO4 )2
Answer:
Ca3 (PO4 )2 s Ōåö 3Ca2+ 3s + 2PO43- 2s
Ksp = [Ca2+]3 [PO43-]2
Ksp = (3s)3 (2s)2
Ksp = 27s3 .4s2
Ksp =108s5
21. A saturated solution, prepared by dissolving CaF2 (s) in water, has [Ca2+] = 3.3 ├Ś10-4M What is the Ksp of CaF2 ?
Answer:
CaF2(s) Ōåö Ca(aq)2+ + 2F -(aq)
[F -] = 2 [Ca2+ ] = 2 ├Ś 3.3 ├Ś10-4 M
= 6.6 ├Ś10-4M
Ksp = [Ca2+][F -]2
= (3.3 ├Ś10-4)(6.6 ├Ś10-4)2
= 1.44 ├Ś10-10
22. Ksp of AgCl is 1.8 ├Ś10ŌłÆ10 . Calculate molar solubility in 1 M AgNO3
Answer:
AgCl (s) Ōåö Ag+ (aq) + Cl- (aq)
x = solubility of AgCl in 1M AgNO3
AgNO3 (aq) Ōåö Ag+ (aq) 1M + NO3-(aq) 1M
[Ag+] = x+1 = 1M (x<<1)
[Cl-] = x
Ksp =[Ag+][Cl-]
1.8 ├Ś 10-10 = (1)(x)
x= 1.8 ├Ś 10-10 M
23. A particular saturated solution of silver chromate Ag2 CrO4 has [Ag+ ]=5 ├Ś10-5 and [CrO4 ]2 -=4.4 ├Ś10 -4 M. What is the value of Ksp for Ag2 CrO4 ?
Answer:
Ag2 CrO4 (s) Ōåö 2Ag+(aq) + CrO42- (aq)
Ksp = [Ag+]2[CrO42-]
= (5├Ś10-5)2 (4.4├Ś10 -4 )
= 1.1├Ś10-12
24. Write the expression for the solubility product of Hg2 Cl2 .
Answer:
Hg2 Cl2 s Ōåö Hg22+ + 2Cl- 2s
Ksp = [Hg22+][Cl-]2
= (s)(2s)2
Ksp =4s3
25. Ksp of Ag2 CrO4 is 1.1├Ś10-12 . what is solubility of Ag2 CrO4 in 0.1M K2 CrO4.
Answer:
Ag2CrO4 x Ōåö 2Ag+ 2x + CrO42- x
x is the solubility
of Ag2 CrO4 in 0.1M K2CrO4
K2CrO4 Ōåö 2K+ + CrO42-
0.1M Ōåö 0.2 M + 0.1 M
[Ag+] = 2x
[CrO42- ] = (x+0.1) Ōēł 0.1 x<<0.1
Ksp = [Ag+]2[CrO42-]
1.1 ├Ś10-12 = (2x)2 (0.1)
1.1 ├Ś10-12 = 0.4x2
x2 = [ 1.1 ├Ś10-12 / 0.4]
x = ŌłÜ[ 1.1 ├Ś10-12 / 0.4]
x= ŌłÜ2.75 ├Ś10-12
x=1.65 ├Ś10-6M
26. Will a precipitate be formed when 0.150 L of 0.1M Pb(NO3)2 and 0.100L of 0.2 M NaCl are mixed? Ksp (PbCl2 )=1.2 ├Ś10-5 .
Answer:
When two are more solution are mixed, the resulting concentrations are differnet from the original.
Total volume = 0.250L
Pb(NO3)2 Ōåö Pb2+ + 2NO3-
0.1 M Ōåö 0.1 M + 0.2 M
Number of moles
Pb2+ = molarity ├Ś Volume of the solution in lit
= 0.1 ├Ś 0.15
[Pb2+ ]mix = 0.1 ├Ś 0.15 / 0.25
= 0.06 M
NaCl Ōåö Na+ + Cl-
0.2 M Ōåö 0.2 M + 0.2 M
No.of moles Cl- = 0.2 ├Ś 0.1
[Cl-]mix = (0.2 ├Ś 0.1) / 0.25 = 0.08 M
Precipitation of PbCl2 (s) occurs if
[Pb2+ ][Cl- ]2 > Ksp
[Pb2+ ][Cl- ]2 =(0.06)(0.08)2
= 3.84 ├Ś10-4
Since ionic product [Pb2+ ][Cl- ]2 >Ksp ,
PbCl2 is precipitated
27. Ksp of Al(OH)3 is 1 ├Ś10-15M . At what pH does 1.0 ├Ś10-3M Al3+ precipitate on the addition of buffer of NH4Cl and NH4OH solution?
Answer:
Al(OH)3 Ōåö Al 3+ (aq)+3OH- (aq)
Ksp = [Al3+][OH-]3
Al(OH)3 precipitates when
[Al3+][OH-]3 >Ksp
(1├Ś10-3)[OH-]3 > 1├Ś10-15
[OH]3 >1├Ś10-12
[OH-] > 1├Ś10-4M
[OH- ] = 1├Ś10-4M
POH = - log10[OH-] = -log(1 ├Ś10-4 )=4
pH = 14-4= 10
Thus, Al (OH)3 precipitates at a pH of 10
Related Topics