Ionic Equilibrium | Chemistry - Buffer Solution | 12th Chemistry : UNIT 8 : Ionic Equilibrium
Chapter: 12th Chemistry : UNIT 8 : Ionic Equilibrium
Buffer Solution
Buffer Solution
Do you know that our blood maintains a constant pH, irrespective of a
number of cellular acid ŌĆō base reactions. Is it possible to maintain a constant
hydronium ion concentration in such reactions? Yes, it is possible due to
buffer action.
Buffer is a solution which consists of a mixture of a weak acid and its
conjugate base (or) a weak base and its conjugate acid. This buffer solution
resists drastic changes in its pH upon addition of a small quantities of acids
(or) bases, and this ability is called buffer action. The buffer containing
carbonic acid (H2 CO3 ) and its conjugate base HCO-3
is present in our blood. There are two types of buffer solutions.
1. Acidic buffer solution : a solution containing a
weak acid and its salt.
Example : solution containing acetic acid and sodium acetate
2. Basic buffer solution : a solution containing a
weak base and its salt.
Example : Solution containing NH4OH and NH4Cl
Buffer action
To resist changes in its pH on the addition of an acid (or) a base, the
buffer solution should contain both acidic as well as basic components so as to
neutralize the effect of added acid (or) base and at the same time, these
components should not consume each other.
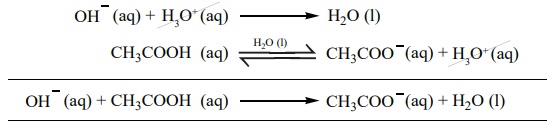
Let us explain the buffer action in a solution containing CH3COOH
and CH3COONa.
The dissociation of the buffer components occurs as below.
CH3COOH (aq) Ōåö CH3 ŌĆō COO-(aq) +
H3O+(aq)

If an acid is added to this mixture, it will be consumed by the
conjugate base CH3COO- to form the undissociated weak
acid i.e, the increase in the concentration of H+ does not
reduce the pH significantly.
CH3COO - (aq) + H+ (aq) ŌåÆ CH3COOH (aq)
If a base is added, it will be neutralized by H3O+,
and the acetic acid is dissociated to maintain the equlibrium. Hence the pH is
not significantly altered.
These neutralization reactions are identical to those reactions that we
have already discussed in common ion effect.
Let us analyse the effect of the addition of 0.01 mol of solid sodium
hydroxide to one litre of a buffer solution containing 0.8 M CH3COOH
and 0.8 M CH3COONa . Assume that the volume change due to the
addition of NaOH is negligible. (Given: Ka for CH3COOH is
1.8 ├Ś10-5
)
The dissociation constant for CH3COOH is given by
Ka =[CH3COO-][H+] / [CH3COOH]
[H+ ]=Ka [CH3COOH ] / [CH3COO-
]
The above expression shows that the concentration of H+ is
directly proportional to
[CH3COOH] / [CH3COO-]
.
Let the degree of dissociation of CH3COOH be ╬▒ then,
[CH3COOH] = 0.8-╬▒ and [CH3COO- ] = ╬▒+0.8
Ōł┤ [H+] = Ka [(0.8-╬▒)/(0.8+╬▒)]
╬▒<<0.8, Ōł┤ 0.8-╬▒ 0.8 and 0.8+╬▒ 0.8
[H+ ] = [Ka (0.8)] / (0.8)
ŌćÆ [H+
]= Ka
Given that
Ka for CH3COOH is 1.8 ├Ś10-5
Ōł┤ [H+] = 1.8 ├Ś10ŌłÆ5 ; pH = - log (1.8 ├Ś10-5 )
=5 - log 1.8
= 5 - 0.26
pH = 4.74
Calculation of pH after adding 0.01 mol NaOH to 1 litre of buffer.
Given that the volume change due to the addition of NaOH is negligible Ōł┤ [OH-]
= 0.01M .
The consumption of OH- are expressed by the following equations.
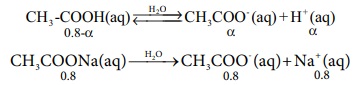
CH3 COOH (aq) ŌåöCH3COO-(aq)
+ H+ (aq)
0.8-╬▒ ╬▒ ╬▒
CH3 COONa(aq) ŌåÆ CH3COO- (aq) + Na+
(aq)
0. 8 0.8 0.8
CH3COOH + OH- (aq) ŌåÆ CH3COO- (aq) + H2O
(l)
Ōł┤ [CH3COOH] = 0.8 - ╬▒ - 0.01 =
0.79 ŌĆō ╬▒
[CH3COO-] = ╬▒+0.8+0.01= 0.81+╬▒ ╬▒<<0.8;
0.79 - ╬▒ = 0.79
and 0.81 + ╬▒ = 0.81
Ōł┤ [H+ ] = (1.8 ├Ś10ŌłÆ5 ) ├Ś (0.79/0.81)
[H+ ] = 1.76 ├Ś10ŌłÆ5
Ōł┤pH = - log ( 1.76 ├Ś10-5 )
=5 - log 1.76
=5 - 0.25
pH = 4.75
The addition of a strong base (0.01 M NaOH) increased the pH only
slightly ie., from 4.74 to 4.75 . So, the buffer action is verified.
Evaluate yourself ŌĆō 8
a. Explain the buffer action in a basic buffer containing
equimolar ammonium hydroxide and ammonium chloride.
b. Calculate the pH of a buffer solution consisting of
0.4M CH3COOH and 0.4M CH3COONa . What is the change in
the pH after adding 0.01 mol of HCl to 500ml of the above buffer solution.
Assume that the addition of HCl causes negligible change in the volume. Given:
( Ka = 1 . 8 ├Ś10ŌłÆ5. )
a) Answer
Dissociation of buffer components
NH4OH (aq) Ōåö NH4+ (aq) + OH-
(aq)
NH4 Cl ŌåÆ NH4+ +Cl+
Addition of H+
The added H+ ions are
neutralized by NH4OH and
there is no appreciable decrease in pH.
NH4OH(aq) + H+
ŌåÆ NH4+ (aq) + H2O(l)
Addition of OHŌĆō
NH4 + (aq) + OH- (aq) ŌåÆ NH4OH (aq)
The added OH- ions react with NH4+ to
produce unionized NH4OH. Since NH4OH is a weak base,
there is no appreciable increase in pH
b) Answer
pH of buffer
CH3COOH(aq) Ōåö CH3COO - (aq) + H
+ (aq)
0.4-╬▒ Ōåö ╬▒ + ╬▒
CH3 COONa(aq) ŌåÆCH 3 COO -
(aq) + Na+ (aq)
0.4 ŌåÆ 0.4 + 0. 4
[H+ ]= K a [CH 3 COOH] / [CH3COO-
]
[CH3COOH] = 0.4 - ╬▒ Ōēł 0.4
[CH3COO- ] = 0.4 + ╬▒ Ōēł 0.4
Ōł┤ [H+] = Ka (0.4) / (0.4)
[H+] = 1.8 ├Ś10-5
Ōł┤ pH = - log (1.8 ├Ś10-5 ) = 4.74
Addition of 0.01 mol HCl to 500ml of buffer
Added [H+ ] =
0.01 mol / 500 mL = 0.01 mol /
1/2L
= 0.02M
CH3 COOH(aq) Ōåö CH3COO- (aq) + H+
(aq)
0.4-╬▒ Ōåö ╬▒ + ╬▒
CH3 COONa ŌåÆ CH3COO- +Na+
0.4 ŌåÆ 0.4 + 0.4
CH3COO- + HCl ŌåÆ CH3COOH+Cl-
(0.02) + 0.02 ŌåÆ 0.02 + 0.02
Ōł┤ [CH3COOH] = 0.4 - ╬▒ + 0.02 = 0.42 - ╬▒ Ōēł 0.42
[CH3COO- ] = 0.4 + ╬▒ - 0.02 = 0.38 + ╬▒ Ōēł 0.38
[H+] = [(1.8 ├Ś 10-5 ) (0.42)] / (0.38)
[H+ ] = 1.99 ├Ś 10-5
pH = - log (1.99 ├Ś10-5 )
= 5 - log 1.99
= 5 - 0.30
= 4.70
Buffer capacity and buffer index
The buffering ability of a solution can be measured in terms of buffer
capacity. Vanslyke introduced a quantity called buffer index, ╬▓, as a
quantitative measure of the buffer capacity. It is defined as the number of
gram equivalents of acid or base added to 1 litre of the buffer solution to
change its pH by unity.

Here,
dB = number of gram equivalents of acid / base added to one litre of
buffer solution.
d(pH) = The change in the pH after the addition of acid / base.
Henderson ŌĆō Hasselbalch equation
We have already learnt that the concentration of hydronium ion in an
acidic buffer solution depends on the ratio of the concentration of the weak
acid to the concentration of its conjugate base present in the solution i.e.,

The weak acid is dissociated only to a small extent. Moreover, due to
common ion effect, the dissociation is further suppressed and hence the
equilibrium concentration of the acid is nearly equal to the initial concentration
of the unionised acid. Similarly, the concentration of the conjugate base is
nearly equal to the initial concentration of the added salt.

Here [acid] and [salt] represent the initial concentration of the acid
and salt, respectively used to prepare the buffer solution
Taking logarithm on both sides of the equation

Example 8.6
Find the pH of a buffer solution containing 0.20 mole per litre sodium
acetate and 0.18 mole per litre acetic acid. Ka for acetic acid is 1.8
├Ś 10-5
.
pH = pKa + log {[salt]/[acid]}
Given that Ka = 1.8 ├Ś 10-5
Ōł┤ pKa = ŌłÆlog(1.8 ├Ś10ŌłÆ5 ) = 5 ŌłÆlog1.8
= 5 -0.26
= 4.74
Ōł┤pH = 4.74 + log (0.20/0.18)
= 4.74 + log (10/9) = 4.74 + log 10 - log 9
= 4.74 + 1 - 0.95 = 5.74 - 0.95
= 4.79
Example 8.7
What is the pH of an aqueous solution obtained by mixing 6 gram of
acetic acid and 8.2 gram of sodium acetate making the volume equal to 500 ml.
(Given: Ka for acetic acid is 1.8 ├Ś 10-5 )
According to Henderson ŌĆō Hasselbalch equation,
pH = pKa + log {[salt]/[acid]}
PKa =-logKa =-log(1.8 ├Ś10-5
)= 4.74 (Refer previous example)
Salt = Number of moles of sodium acetate / Volume of the solution ( litre )
Number of moles of sodium acetate = mass of sodium acetate / molar mass
of sodium acetate

pH = 4.74 + log 1
pH = 4.74 + 0 = 4.74
Evaluate yourself ŌĆō 9
a. How can you prepare a buffer solution of pH 9. You are
provided with 0.1M NH4OH solution and ammonium chloride crystals.
(Given: pKb for NH4OH is 4.7 at 25 C .
b. What volume of 0.6M sodium formate solution is required
to prepare a buffer solution of pH 4.0 by mixing it with 100ml of 0.8M formic
acid. (Given: pKa for formic acid is 3.75. )
a) answer
pOH = pKb +
log ([salt]/[base])
We know that
pH + pOH = 14
Ōł┤ 9 + pOH = 14
ŌćÆ pOH = 14 - 9 = 5
5 = 4.7 + log ([NH4Cl]/[NH4OH])
0.3=log ( [NH4Cl]/0.1)
[NH4Cl] / 0.1
= antilog of (0.3)
[NH4Cl] = 0.1M ├Ś 1.995
= 0.1995 M
= 0.2M
Amount of NH4Cl required to prepare 1 litre 0.2M
solution
= Strength of NH4Cl
├Ś molar mass of NH4Cl
= 0.2 ├Ś 53.5
= 10.70 g
10.70 g ammonium
chloride is dissolved in water and the solution is made up to one litre to get
0.2M solution. On mixing equal volume of the given NH4OH solution
and the prepared NH4Cl solution will give a buffer solution with
required pH value (pH = 9).
b) answer
pH = pKa
+log ( [salt]/[acid] )
4 = 3.75+log ([sodium formate] /[formic acid])
[Sodium formate] =
number of moles of HCOONa = 0.6 ├Ś V ├Ś 10ŌłÆ3
[formic acid] =
number of moles of HCOOH
= 0.8 ├Ś 100 ├Ś 10ŌłÆ3
= 80 ├Ś 10ŌłÆ3
4 = 3.75 + log
(0.6V/80)
0.25 = log
(0.6V/80)
antilog of 0.25 =
0.6V/80
0.6V = 1.778 ├Ś 80
= 1.78 ├Ś 80
= 142.4
V = 142.4 mL / 0.6
= 237.33mL
Related Topics