Answer the following questions

Chemistry : Ionic Equilibrium

Answer the following questions:

1. What are Lewis acids and bases? Give two example for each.

• A Lewis acid is a positive ion (or) an electron deficient molecule Example: BF₃, CO₂, Fe³⁺

• A Lewis base is anion (or) neutral molecule with at least one lone pair of electrons

Example: NH₃, F⁻, Acetylene

2. Discuss the Lowry – Bronsted concept of acids and bases.

• An acid is defined as a substance that has a tendency to donate a proton to another substance (a proton donor)

• A base is a substance that has a tendency to accept a proton form other substance (a proton acceptor)

• Hydrogen chloride is dissolved in water, HCl behaves as an acid and H₂O is base.

HCl + H₂O ⇌ H₃O⁺ + Cl⁻

Proton donar (acid) + Proton acceptor (Base) ⇌ Proton donar (acid) + Proton acceptor (Base)

3. Indentify the conjugate acid base pair for the following reaction in aqueous solution

i) HS- (aq) + HF ↔ F- (aq) + H2 S(aq)

ii) HPO42- + SO32- ↔ PO43- + HSO3-

iii) NH4+ + CO32- ↔ NH3 + HCO3

i) HS⁻ (aq) + HF ⇌ F⁻(aq) + H₂S(aq)

ii) HPO₄²⁻ + SO₃²⁻ ⇌ PO₄³⁻ + HSO₃⁻

iii) NH₄⁺ + CO₃²⁻ ⇌ NH₃ + HCO₃⁻

i) HS⁻ (aq) + HF ⇌ F⁻ (aq) + H₂S(aq) 

• HF donates a proton to HS⁻ and gives F⁻. HF is acid. Hence the conjugate base of HF is F⁻.

• HS⁻ accepts a proton from HF and forms H₂S. HS⁻ is base and its conjugate acid is H₂S.

ii) HPO₄²⁻ + SO₃²⁻ ⇌ PO₄³⁻ + HSO₃⁻

• HPO₄²⁻ donates a proton to SO₃²⁻. HPO₄²⁻ is acid. Hence its conjugate base is PO₄³⁻

• SO₃²⁻ accepts a proton from HPO₄²⁻. SO₃²⁻ is base. Hence its conjugate acid is HSO⁻₃.

iii) NH₄⁺ + CO₃²⁻ ⇌ NH₃ + HCO₃⁻

• NH₄⁺ donates a proton to CO₃²⁻. NH₄⁺ is acid. Hence its conjugate base is NH₃.

• CO₃²⁻ accepts a proton from NH₄⁺. CO₃²⁻ is base. Hence its conjugate acid is HCO⁻₃.

4. Account for the acidic nature of HClO4 in terms of Bronsted – Lowry theory, identify its conjugate base.

• HClO₄ having the tendency to donate a proton. Hence it is acidic in nature.

• HClO₄⁻ + H₂O ⇌ H₃O⁺ + ClO₄⁻

perchloric acid + water ⇌ Hydronium ion + chlorate ion

• HClO₄ donates a proton to H₂O and forms H₃O⁺ and ClO₄⁻

• ClO₄⁻ is the conjugate base of HClO_4.

5. When aqueous ammonia is added to CuSO4 solution, the solution turns deep blue due to the formation of tetramminecopper (II) complex, [Cu(H2 O)4 ](aq)2+ +4NH3 (aq) ↔ [Cu(NH3)4 ](aq)2+ , among H2O and NH3 Which is stronger Lewis base.

Ammonia was added to the aqueous CuSO₄ solution and forms tetramine Cu (II) complex.

Water present in the coordination sphere was replaced by NH₃ and the complex formed. Moreover the higher electronegativity of oxygen also responsible for less availability of lone pair of electrons on the oxygen atom. [Hence NH₃ is strong and Lewis base than H₂O]

6. The concentration of hydroxide ion in a water sample is found to be 2.5 ×10-6 M .. Identify the nature of the solution.

[OH⁻] = 2.5 × 10^-6 M

 pOH = -ℓog (2.5 × 10⁻⁶)

= −ℓog₁₀2.5 + 6 ℓog₁₀l0

 = −0.3979 + 6 = 5.6021

pOH = 5.6021

pH + pOH = 14

pH = 14 − 5.6021 = 8.3979 = 8.4

Hence the solution is Basic

7. A lab assistant prepared a solution by adding a calculated quantity of HCl gas at 25oC to get a solution with [H3O+ ] = 4 ×10-5M . Is the solution neutral (or) acidic (or) basic.

[H₃0⁺] = 4 × 10⁻⁵ M

 pH = −ℓog [H₃O⁺]

= −log (4 × l0⁻⁵)

= −log 4 + 5 log 10

 pH = −0.6020 + 5 = 4.3979

 pH = 4.4

The solution is acidic

8. Calculate the pH of 0.04 M HNO3 Solution.

Solution:

Concentration of HNO3 = 0.04M

[H3O +] = 0.04 mol dm-3

pH = -log[H3O+]

 = -log(0.04)

 = -log(4 ×10-2 )

= 2-log4

=2-0.6021

=1.3979 = 1.40

9. Define solubility product

The solubility product of a compound is defined as the product of the molar concentration of the constituent ions, each raised to the power of its stoichiometric co-efficient in a balanced equilibrium equation.

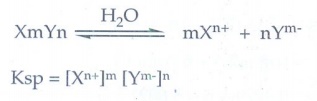
10. Define ionic product of water. Give its value at room temperature.

2H₂O ⇌ H₃O⁺ + OH⁻

According to law of mass action,

K _eq = ( [H₃O⁺] [OH⁻] ) / ( [H₂O]²)

∴ K _eq = [H₂O]² = [H₃O⁺] [OH⁻]

K_w = l × 10⁻¹⁴ mol² dm^{− 6}

The constant K_w is known as ionic product of water and it is given by the product of concentrations of [H₃0⁺] and [OH⁻] ions at 298 K.

11. Explain common ion effect with an example

• When a salt of a weak acid is added to the acid itself, the dissociation of the weak acid is suppressed further.

• Example: Addition of sodium acetate to acetic acid solution.

• The acetic acid dissociated weakly. The common ion, CH₃COO⁻ suppress the dissociation of acetic acid

CH₃COOH(aq) ⇌ H ⁺(aq) + CH₃ COO⁻ (aq)

acetic acid ⇌ Hydrogen ion + acetate ion

• The added sodium acetate, salt completely dissociates to produce Na⁺ and CH₃COO⁻ ion.

• To maintain the equilibrium, the excess CH₃COO⁻ ions combines with H⁺ ions to produce much more unionized CH₃COOH and dissociation of CH₃COOH suppressed.

12. Derive an expression for Ostwald’s dilution law

Ostwald dilution law relates the dissociation constant of the weak electrolyte with degree of dissociation and the concentration of the weak electrolyte

CH₃COOH ⇌ CH₃COO⁻ + H⁺

Ka = ( [CH₃ COO⁻][H⁺] ) / [CH₃COOH]

∝ = degree of dissociation

K_a = Cα.Cα / C(l-α) = α².c² / C(l−α) = α².C / l−α

If α is too small K_a = α²c

Calculation for degree of dissociation (α):

α² = k_c/c , α = √[k_a/c]

Calculation for concentration:

[H⁺] = [CH₃COO⁻] = Cα

C. √[ka/c] = √C . √K_a = √[K_a. C]

∴ K_a = α²C / 1− α is known as the Ostwald’s dilution law.

13. Define pH

pH of a solution is defined as the negative logarithm of base 10 of the molar concentration of the hydronium ions present in the solution.

pH = −log₁₀[ H₃0⁺]

14. Calculate the pH of 1.5×10-3M solution of Ba (OH)2

Answer:

Ba(OH)₂ → Ba²⁺ + 2OH⁻

1.5 × 10⁻³ M → 2 × 1.5 × 10⁻³ M.

[OH⁻] = 3 × 10⁻³M

[∵ pH + pOH = 14]

pH = 14 − pOH

pH = 14 − (−log[OH⁻])

= 14 + log [OH⁻]

= 14 + log (3 × l0⁻³)

= 14 + 0.4771−3

= 11 + 0.4771

 pH = 11.48

15. 50ml of 0.05M HNO3 is added to 50ml of 0.025M KOH . Calculate the pH of the resultant solution.

Answer:

Number of moles of HNO₃ = 0.05 × 50 × l0⁻³

= 2.5 × 10⁻³

Number of moles of KOH = 0.025 × 50 × 10⁻³

= 1.25 × 10⁻³

Number of moles of HNO₃ after mixing

= 2.5 × 10⁻³ − 1.25 × 10⁻³

= 1.25 × 10⁻³

∵ Concentration of HNO₃

= Number of moles of HNO₃ / Volume in litre

After mixing, total volume = 100 ml

= 100 × 10⁻³ L

∵ [H⁺] = (1.25 × 10⁻³ moles) / (100 × 10⁻³L)

= 1.25 × 10⁻² moles L⁻¹

pH = −log [H⁺]

pH = −log₁₀(1.25 × 10⁻²)

= −log₁₀ l.25 + 21og₁₀l0              [log₁₀ l0 = l ]

pH = −0.0969 + 2 = 1.9031

16. The Ka value for HCN is 10-9 . What is the pH of 0.4M HCN solution?

Given:

K_a =10⁻⁹

c = 0.4 M

pH = −log[H⁺]

[H⁺] = √[K_a × c] = √[10^-9 × 0.4] = 2 × 10^-5

 ∴ pH = −log₁₀(2 ×l0⁻⁵)

= log₁₀2 + 5 log₁₀ 10 = −0.3010 + 5 = 4.699

 pH = 4.699

17. Calculate the extent of hydrolysis and the pH of 0.1 M ammonium acetate Given that Ka =Kb =1.8 ×10-5

Answer:

h = √K_h = √[ K_w / (K_aK_b) ] = √[(1x10⁻¹⁴)/(1.8 × 10^-5 × 1.8 × 10^{- 5})]

= √ [ (l/1.8) × 10^-4 ] = √0.5555×10^-4

= 0.7453×10^-2

pH = 1/2 pK_w + 1/2 PK_a – 1/2 PK_b

 Given that K_a = K_b = 1.8 × 10⁻⁵

 If K_a = K_b , then pK_a = pK_b

∴ pH = l/2 pK_w = 1/2 (14) = 7

18. Derive an expression for the hydrolysis constant and degree of hydrolysis of salt of strong acid and weak base

Let us consider the reactions between a strong acid, HCl, and a weak base, NH₄OH, to produce a salt, NH₄Cl and water

 HCl(aq) + NH₄OH(aq) ⇌ NH₄Cl(aq)+H₂O(ℓ)

For strong acid

[H⁺] > [OH⁻]; the solution is acidic and the pH is less than 7.

K_h.K_b = K_w

K_h = K_w/K_b

Kh = h²C

[H⁺] =√[K_h.C]

substitute K_h value in the above equation

[H⁺] = √{K_w/K_b . C}

pH = −ℓog₁₀[H⁺]

 = − log (K_w.C/ K_b)^1/2

= − 1/2 log K_w−1/2 log C + 1/2 log K_b

PH = 7 - l/2pK_b − l/2 log C 

19. Solubility product of Ag2CrO4 is 1 ×10-12 . What is the solubility of Ag2 CrO4 in 0.01M AgNO3 solution?

Answer:

Given that Ksp =1 × 10-12

Ag2 CrO4 (s) ↔ 2 Ag+(aq) + CrO4−2 (aq)

 s ↔ 2s + s

AgNO3 (s) ↔ Ag+(aq) + NO3- (aq)

 0.01M ↔ 0.01M + 0.01M

[Ag+] = 2s + 0.01     

0.01>>2S 

∴ [Ag+ ]= 0.01M

[CrO42−]= s

Ksp = [Ag+]2 [CrO42- ]

1 × 10-12 = (0.01)2 (s)

(s) = 1 × 10-12 / (10-2)2 = 1 × 10−8 M

20. Write the expression for the solubility product of Ca3 (PO4 )2

Answer:

Ca₃(PO₄)₂ ⇌ 3Ca²⁺ + 2PO₄^3-

     s                    3s           2s

K_sp = [Ca²⁺]³ [PO₄³⁻]²

K_sp = (3s)³ (2s)²

K_sp = 27s³. 4s²

 K_sp = 108 s⁵

21. A saturated solution, prepared by dissolving CaF2 (s) in water, has [Ca2+] = 3.3 ×10-4M What is the Ksp of CaF2 ?

Answer:

CaF₂(s) ⇌ Ca_(aq)²⁺ + 2F⁻ (aq)

[F⁻] = 2 × 3.3 × 10^-4 M

= 6.6 × 10⁻⁴ M

K_sp = [Ca²⁺][F⁻]²

 = (3.3 × 10⁻⁴) (6.6 × 10⁻⁴)²

 = 1.44 × 10⁻¹⁰

22. Ksp of AgCl is 1.8 ×10−10 . Calculate molar solubility in 1 M AgNO3

Answer:

AgCl(s) ⇌ Ag⁺(aq) + Cl⁻ (aq)

x = solubility of AgCl in 1M AgNO₃

AgNO_3(aq) ⇌ Ag+(aq) [1M] + NO₃⁻ (aq) [1M]

 [Ag⁺] = x + 1       1M (∵ x < < 1)

[Cl⁻] = x

K_sp = [Ag⁺] [Cl⁻]

1.8 × 10⁻¹⁰ = (1) (x)

 x = 1.8 × 10⁻¹⁰ M

23. A particular saturated solution of silver chromate Ag2 CrO4 has [Ag+ ]=5 ×10-5 and [CrO4 ]2 -=4.4 ×10 -4 M. What is the value of Ksp for Ag2 CrO4 ?

Answer:

Ag₂CrO₄(s) ⇌ 2Ag⁺_(aq) + CrO₄²⁻_(aq)

K_sp = [Ag⁺]² [CrO₄²⁻]

= (5 × l0^-5)² (4.4 × 10⁻⁴) = (25×10⁻¹⁰) 4.4 × l0⁻⁴

 = 1.1 × 10⁻¹² = 110 × 10⁻¹⁴

 = 1.10 × 10⁻¹²

24. Write the expression for the solubility product of Hg2 Cl2 .

Answer:

Hg₂Cl₂ ⇌ Hg₂²⁺ + 2Cl⁻

     s            s         2s

K_sp = [Hg₂²⁺] [Cl⁻]²

= (s) (2s)²

K_sp = 4s³

25. Ksp of Ag2 CrO4 is 1.1×10-12 . what is solubility of Ag2 CrO4 in 0.1M K2 CrO4.

Answer:

Ag₂CrO₄ ⇌ 2Ag⁺ + CrO₄²⁻

   x                2x           x

x is the solubility of Ag₂CrO₄ in 0.1 M K₂CrO₄

K₂CrO₄ ⇌ 2K⁺ + CrO₄²⁻

 0.1 M            0.2 M        0.1 M

[Ag⁺] = 2x

[CrO₄²⁻] = (x + 0.1) ≈ 0.1          ∵ x < < 0.1

K_sp = [Ag⁺]² [CrO₄²⁻]

1.1 × 10⁻¹² = (2x)² (0.1)

1.1 × 10⁻¹² = 0.4 x²

 x² = [1.1×10⁻¹²] / 0.4 ; x = √[1.1 × 10⁻¹²] / [0.4]

 x = √(2.75 × 10⁻¹²)

 x = 1.65 × 10⁻⁶ M

26. Will a precipitate be formed when 0.150 L of 0.1M Pb(NO3)2 and 0.100L of 0.2 M NaCl are mixed? Ksp (PbCl2 )=1.2 ×10-5 .

Answer:

When two or more solutions are mixed, the resulting concentrations are different from the orignal.

Total volume = 0.150 L

Pb(NO₃)₂ ⇌ Pb²⁺ + 2NO⁻₃

 0.1 M       0.1M      0.2 M

Number of moles

Pb²⁺ = molarity × Volume of the solution in liter

 = 0.1 × 0.15

[Pb²⁺]_mix = (0.1 × 0.15) / 0.25 = 0.06 M

NaCl    ⇌   Na⁺     +    Cl⁻

0.2 M        0.2M    0.2M

No. of moles Cl⁻ = 0.2 × 0.1

[Cl⁻]_mix = (0.2 × 0.1) / 0.25 = 0.08 M

Precipitation of PbCl_{2 (s)} occurs if

[Pb²⁺] [Cl⁻]² > K_sp

[Pb²⁺] [Cl⁻]² = (0.06) (0.08)²

= 3.84 × 10⁻⁴

Since ionic product [Pb²⁺] [Cl⁻]² > K_sp , PbCl₂ is precipitated

27. Ksp of Al(OH)3 is 1 ×10-15M . At what pH does 1.0 ×10-3M Al3+ precipitate on the addition of buffer of NH4Cl and NH4OH solution?

Answer:

Al(OH)₃ ⇌ Al³⁺_(aq) + 3OH⁻_(aq)

K_sp = [A𝑙³⁺] [OH⁻]³

Al(OH)₃ precipitates when 

[Al³⁺] [OH⁻]³ > K_sp

(l ×10⁻³) [OH⁻]³ > 1 × 10⁻¹⁵

[OH⁻]³ > 1 × 10⁻¹²

[OH⁻] > 1 × 10^-4 M

[OH⁻] = l× 10^-4 M

pOH = −log₁₀[OH⁻]= −log(1×10⁻⁴) = 4

pH = 14 − 4 = 10

Thus, Al(OH)₃ precipitates at a pH of 10

EVALUATE YOURSELF:

1. Classify the following as acid (or) base using Arrhenius concept

i) HNO₃ ii) Ba(OH)₂ iii) H₃PO₄ iv) CH₃COOH

Answer:

acid: i) HNO₃ iii) H₃PO₄ iv) CH₃COOH

base: ii) Ba(OH)₂

2. Write a balanced equation for the dissociation of the following in water and identify the conjugate acid-base pairs.

i) NH₄⁺ ii) H₂SO₄ iii) CH₃COOH

Answer:

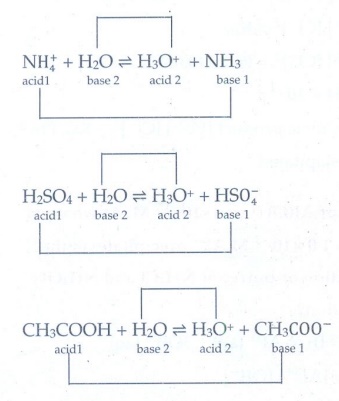
NH₄⁺   +       H₂O      ⇌       H₃O⁺   +   NH₃

acid l         base 2              acid 2      base 1

H₂SO₄ + H₂O ⇌ H₃O⁺ + HSO₄^-

acid l    base 2   acid 2   base 1

CH₃COOH + H₂O ⇌ H₃O⁺ + CH₃COO^-

     acid l     base 2    acid 2      base 1

3. Identify the Lewis acid and the Lewis base in the following reactions.

a) CaO + CO₂ —> CaCO₃

 CH3 Cl

b) CH₃ - O - CH₃ + AlCl₃ →

Answer:

i) CaO - Lewis base ; CO₂ - Lewis acid

ii) 

AlCl₃ - Lewis acid

4. H₃BO₃ accepts hydroxide ion from water as shown below

H₃BO₃(aq) + H₂O(ℓ) ⇌ B(OH)₄^- + H⁺

Predict the nature of H₃BO₃ using Lewis concept

5. At a particular temperature, the K_w of a neutral solution was equal to 4xl0⁻¹⁴. Calculate the concentration of [H₃O⁺] and [OH^-].

Given solution is neutral

∴ [H₃O⁺] = [OH⁻]

Let [H₃O⁺] = x; then [OH⁻] = x

 K_W = [H₃O⁺] [OH⁻]

4 × 10⁻¹⁴ = x . x

x² = 4 × 10⁻¹⁴

x = √[4×10⁻¹⁴] = 2 × 10^-7

6. a) Calculate pH of 10⁻⁸ H₂SO₄

b) Calculate the concentration of hydrogen ion in moles per litre of a solution whose pH is 5.4 

c) Calculate the pH of an aqueous solution obtained by mixing 50 ml of 0.2 M HCl with 50ml 0.1 M NaOH.

a)

In this case the concentration of H₂SO₄ is very low and hence [H₃O⁺] from water cannot be neglected

 ∴ [H₃O⁺] = 2 × 10⁻⁸ (from H₂SO₄) + 10^-7 (from water)

= 10⁻⁸ (2 + 10)

= 12 × 10⁻⁸ = 1.2 × 10⁻⁷

pH = −log₁₀[H₃O⁺]

= −log₁₀ (1.2 × l0⁻⁷)

= 7 − log₁₀ 1.2

pH = 7 − 0.0791 = 6.9209

b)

pH of the solution = 5.4

[H₃O⁺] = antilog of (-pH)

= antilog of (−5.4)

= antilog of (−6 + 0.6)

= 3.981 × 10⁻⁶

[H₃O⁺] = 3.98 × 10⁻⁶ mol dm⁻³

c)

No of moles of HCl = 0.2 × 50 × 10⁻³ = 10 × l0⁻³

No of moles of NaOH = 0.1 × 50 × l0⁻³ = 5 × l0⁻³

No of moles of HCl after mixing

= (10 × l0⁻³ ) – (5 × 10⁻³)

= 5 × 10⁻³

After mixing total volume = 100 mL

 ∴ Concentration of HCl in moles per litre

= [5 × 10⁻³ mole] / [100 × 10⁻³L]

[H₃O⁻] = 5 × 10⁻² M

pH = −log₁₀ (5 × l0⁻²) = −log₁₀5 + 21og₁₀10

 = 2 − log5 = 0.6990 + 2

= 2 − 0.6990 = 1.3010

= 1.30

pH = 1.3

7. K_b for NH₄OH is 1.8 × 10^-5. Calculating the percentage of ionisation of 0.06 M ammonium hydroxide solution.

α = √[K_b / C ] = √[1.8 × 10⁻⁵ ] / [ 6 × 10⁻² ] = √(3 × 10^-4)

= 1.732 × 10⁻²

= 1.732 / 100 = 1.732 %

8. a) Explain the buffer action in a basic buffer containing equimolar ammonium hydroxide and ammonium chloride.

b) Calculate the pH of a buffer solution consisting of 0.4M CH₃COOH and 0.4M CH₃COONa. What is the change in the pH after adding 0.01 mol of HCl to 500 ml of the above buffer solution. Assume that the addition of HCl causes negligible change in the volume.

Given:

(K_a = 1.8 × l0^-5).

a) Dissociation of buffer components

NH₄OH (aq) ⇌ NH₄⁺ (aq) + OH⁻ (aq)

NH₄Cl → NH₄⁺ + Cl⁻

Addition of H⁺

The added H⁺ ions are neutralized by NH₄OH and there is no appreciable decrease in pH.

NH₄OH(aq) + H⁺ → NH₄⁺ (aq) + H₂O (ℓ)

Addition of OH⁻

The added OH⁻ ions react with NH₄⁺ to produce unionized NH₄OH. Since NH₄OH is a weak base, there is no appreciable increase in pH

NH₄⁺ (aq) + OH⁻ (aq) → NH₄OH (aq)

b)

pH of buffer

CH₃COOH (aq) ⇌ CH₃COO⁻ (aq) + H⁺ (aq)

      0.4 – α                   α                     α

CH₃COONa (aq) → CH₃COO⁻ (aq) + Na⁺ (aq)

[H⁺] = K_a[CH₃COOH] / [CH₃C00⁻]

[CH₃COOH] = 0.4 − α ≃ 0.4

[CH₃COO⁻] = 0.4 − α ≃ 0.4

∴ [H⁺] = K_a(0.4) / (0.4)

[H⁺] = 1.8 × 10^-5

∴ pH = −log (1.8 × l0^-5) = 4.74

Addition of 0.01 mol HCl to 500 ml of buffer

Added [H⁺] = 0.01 mol / 500 ml. = 0.01 mol / ½ L

= 0.02 M

CH₃COOH(aq) ⇌ CH₃COO⁻ (aq) + H⁺(aq)

0.4 - α                         α                    α

CH₃COONa → CH₃COO⁻ + Na⁺

0.4                      0.4            0.4

CH₃COO⁻ + HCl → CH₃COOH + C𝑙⁻

(0.02)          0.02           0.02        0.02

∴ [CH₃COOH] = 0.4 − α + 0.02 = 0.42 − α ≃ 0.42

 [CH₃COO⁻ ] = 0.4 + α − 0.02 = 0.38 + α ≃ 0.38

[H⁺] = [ (l.8 × l0^-5) (0.42) ] / (0.38)

[H⁺] = 1.99 × 10^-5

pH = −log (1.99 × 10^-5)

= 5 − log 1.99

 = 5 − 0.30 = 4.70

9. a) How can you prepare a buffer solution of pH 9. You are provided with 0.1M NH₄OH solution and ammonium chloride crystals. (Given: pK_a for NH₄OH is 4.7 at 25° C).

b) What volume of 0.6 M sodium formate solution is required to prepare a buffer solution of pH 4.0 by mixing it with 100ml of 0.8M formic acid. (Given: pK_a for formic acid is 3.75).

a) pOH = pK_b + log ( [salt] / [base] )

pH + pOH = 14

∴ 9 + pOH = 14

⇒ pOH = 14 − 9 = 5

5 = 4.7 + log ( [NH₄Cl] / [NH₄OH] )

0.3 = log ( [NH₄Cl] / 0.1)

[NH₄Cl] / 0.1 = antilog of (0.3)

[NH₄Cl] = 0.1 M × 1.995

= 0.1995 M

= 0.2 M

Amount of NH₄Cl required to prepare 1 litre 0.2M solution

= strength of NH₄Cl × molar mass of NH₄Cl

 = 0.2 × 53.5

 = 10.70 g

10.70 g ammonium chloride is dissolved in water and the solution is made up of one litre to get 0.2 M solution. On mixing equal volume of the given NH₄OH solution and the prepared NH₄Cl solution will give a buffer solution with required pH value (pH = 9).

b)

PH = pK_a + log ( [salt] / [base] )

4= 3.75 + log ([sodium formate] / [formic acid])

[sodium formate] = Number of moles of HCOONa / Volume of HCOONa

= 0.6 × V × 10⁻³

[Formic acid] = Number of moles of HCOOH / Volume of HCOOH

= 0.8 × 100 × 10⁻³

= 80 × 10⁻³

4 = 3.75 + log (0.6 V / 80)

0.25 = log (0.6 V / 80)

antilog of 0.25 = 0.6 V / 80

0.6 V = 1.778 × 80

= 142.4

V = 142.4 mL / 0.6 = 237.33 mL

10. Calculate the i) hydrolysis constant,

ii) degree of hydrolysis and iii) pH of 0.05M sodium carbonate solution pK_a for HCO⁻³ is 10.26.

Sodium carbonate is a salt of weak acid, H₂CO₃ and a strong base, NaOH and hence the solution is alkaline due to hydrolysis.

Na₂CO₃(aq) → 2Na⁺ (aq) + CO₃²⁻ (aq)

CO₃²⁻ (aq) + H₂O(ℓ) ⇌ HCO₃⁻ + OH⁻

i) h = √[K_w / (K_a×C) ]

 = √(1 × 10⁻¹⁴) / (1.8 × 10 ⁻⁵ × 0.1)

h = 7.5 × 10⁻⁵

 Given that pKa = 4.74

pK_a = −log K_a

ie., K_a = antilog of (−pK_a)

= antilog of (−4.74)

= antilog of (−5 + 0.26)

= 10⁻⁵ × 1.8

[antilog of 0.26 = 1.82 ≃1.8]

ii) K_h = K_w / K_a = 1×10⁻¹⁴ / 1.8×10^-5

 K_h = 5.56 × 10⁻¹⁰

iii) pH = 7 + pK_a /2 + logC/2

 pH = 7 + (4.74/2) + (log 0.1 / 2) = 7 + 2.37 − 0.5

 = 8.87