Book Back and Important Questions Answers | Chemistry - Solid State: Answer the following questions | 12th Chemistry : UNIT 6 : Solid State
Chapter: 12th Chemistry : UNIT 6 : Solid State
Solid State: Answer the following questions
Chemistry : Solid State
Answer the following questions:
1. Define unit cell.
• A basic repeating structural unit
of a crystalline solid is called a unit cell.
• A unit cell is characterised by
the three edge lengths (a, b, c) or lattice constants and the angle between the
edges α, β and γ.
2. Give any three characteristics of ionic crystals.
1.
Ionic solids have high melting point.
2.
These solids do not conduct electricity, because the ions are fixed in their
lattice positions.
3.
They conduct electricity in molten state (or) when dissolved in water because,
the ions are free to move in the molten state or solution.
4.
They are hard as only strong external force can change the relative positions
of ions
3. Differentiate crystalline solids and amorphous solids.
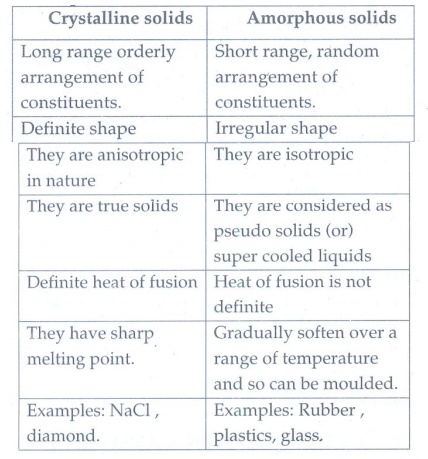
Crystalline solids
•
Long range orderly arrangement of constituents.
•
Definite shape
•
They are anisotropic in nature
•
They are true solids
•
Definite heat of fusion
•
They have sharp melting point.
•
Examples: NaCl, diamond.
Amorphous solids
•
Short range, random arrangement of constituents.
•
Irregular shape
•
They are isotropic
•
They are considered as pseudo solids (or) super cooled liquids
•
Heat of fusion is not definite
•
Gradually soften over a range of temperature and so can be moulded.
•
Examples: Rubber, plastics, glass.
4. Classify the following solids
a. P4 b. Brass c. diamond d. NaCl e. Iodine
a)
P4 - Covalent solid
b)
Brass - Metallic solid
c)
Diamond - Covalent solid
d)
NaCl - Ionic solid
e)
Iodine - Molecular solid
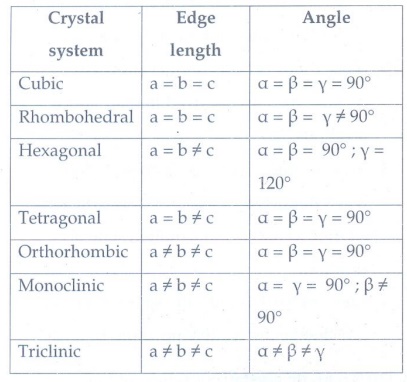
5. Explain briefly seven types of unit cell.
6. Distinguish between hexagonal close packing and cubic close packing.

Hexagonal close Packing
• The
spheres can be arranged so as to fit into the depression in such a way that the
third layer placed directly over a first layer
•
abab arrangement is known as the hexagonal close packed (hcp) arrangement
•
The tetrahedral voids of the second layer are covered by the spheres of the
third layer
•
The coordination number is 12
Cubic close packing
•
The third layer may be placed over the second layer in such a way that all the
spheres of the third layer fit in octahedral voids
•
abcabcabc... arrangement is called cubic close packed (ccp) structure.
•
The octahedral voids of the second layer are covered by the spheres of the
third layer
•
The coordination number is 12
7. Distinguish tetrahedral and octahedral voids.

Tetrahedral voids
•
During the crystal layer arrangement wherever a sphere of the second layer is
above the void of the first layer a tetrahedral void is formed. These voids are
called tetrahedral voids
•
The void is surrounded by 4 spheres
•
Radius of an tetrahedral voids r / R = 0.225
Octahedral voids
•
The triangular voids in the second layer are above the triangular voids in the
first layer, and these are not overlap.
•
The void is surrounded by 6 sphere
•
Radius of a octahedral void r / R = 0.414
8. What are point defects?
If
the deviation occurs from the perfect crystal is due to missing atoms,
displaced atoms or extra atoms, the imperfection is named as a point defect.
Such
defects arise due to imperfect packing during the original crystallisation or
they may arise from thermal vibrations of atoms at elevated temperatures.
Example:
Schottky defect and Frenkel defect.
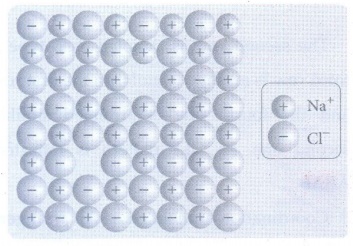
9. Explain Schottky defect.
• Schottky defect arises due to the
missing of equal number of cations and anions from the crystal lattice.
• This defect does not change the
stoichiometry of the crystal.
• Ionic solids in which the cation
and anion are of almost of similar size show schottky defect. Example: NaCl.
• Schottky defects in a crystal,
lowers its density.
• For example, the theoretical
density of vanadium monoxide (VO) is 6.5 g cm−3, but the actual experimental
density is 5.6 g cm −3.
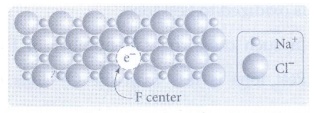
10. Write short note on metal excess and metal deficiency defect with an example.
Metal excess defect
• Metal excess defect arises due to
the presence of more number of metal ions as compared to anions.
• The electrical neutrality of the
crystal can be maintained by the presence of anionic vacancies equal to the
excess metal ions (or) by the presence of extra cation and electron present in
interstitial position.
•
Example:
When NaCl crystals are heated in the presence of sodium vapour, Na+
ions are formed and are deposited on the surface of the crystal.
• Chloride ions (CƖ−) diffuse to the surface
from the lattice point and combines with Na+ ion. The electron lost
by the sodium vapour diffuse into the crystal lattice and occupies the vacancy
created by the CƖ − ions.
• Such anionic vacancies which are
occupied by unpaired electrons are called F centers.
• The formula of NaCl which
contains excess Na+ ions can be written as Na1+xCl.
Metal deficiency defect
• Metal deficiency defect arises
due to the presence of less number of cations than the anions.
• This defect is observed in a
crystal in which, the cations have variable oxidation states.

• Example: FeO crystal, some of the
Fe2+ ions are missing from the crystal lattice.
• To maintain the electrical
neutrality, twice the number of other Fe2+ ions in the crystal is
oxidized to Fe3+ ions.
• In such cases, overall number of
Fe2+ and Fe3+ ions is less than the O2− ions.
It was experimentally found that the general formula of ferrous oxide is FexO,
where x ranges from 0.93 to 0.98.
11. Calculate the number of atoms in a fcc unit cell.

• Identical atoms present at each
corner as well as in the centre of each face.
• The atom in the face centre is
shared by two unit cells.
• Each corner atom shared by 8 unit cells and makes 1/8 contribution to the unit cell.
Number
of atoms in a fcc unit cell = (Nc / 8) + (Nf / 2)
=
(8 / 8) + (6 / 2)
=
1+3 = 4
12. Explain AAAA and ABABA and ABCABC type of three dimensional packing with the help of neat diagram.
(i) AAA... type
(i)
Linear arrangement of spheres in one direction is repeated in two dimension
(ii)
All spheres of different rows align vertically as well as horizontally in
identical pattern
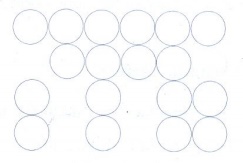
All the rows are identical and the packing is
called AAA type. In this arrangement each sphere is in contact with four of its
neighbours.
(ii) ABAB.. Type
In
this type, the second row spheres are arranged in such a way that they fit in
the depression of the first row.
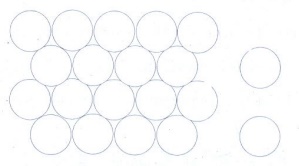
The
second row is denoted as B type. The third row is arranged similar to the first
row A, and the fourth one is arranged similar to second one. i.e., the pattern
is repeated as ABAB....
Coordination
number of ABAB arrangement is 6.
(iii) ABCABC type
Formation of first layer
The
first layer is formed by arranging two dimensional ABAB arrangements i.e. the
spheres of second row fit into the depression of first row.
Formation of second layer
In
the first layer (A) there are two types of voids (or holes) and they are
designated as x and y. The second layer (B) can be formed by placing the
spheres either on the depression (voids / holes) x (or) on y. Consider the
formation of second layer by placing the spheres on the depression (y).
The
voids (y) in the first layer (A) are partially covered by the spheres of layer
(B), now such a void in (A) is called a octahedral void. This constitutes six
spheres - three in the lower layer (A) and three in the upper layer (B). When
the centers of these six spheres are joined, an octahedron is formed. Simultaneously
new tetrahedral voids (or holes) are also created by three spheres in second
layer (B) and one sphere of first layer (A)
Formation of third layer
The
third layer may be placed over the second layer in such a way that all the
spheres of the third layer fit in octahedral voids. This arrangement of the
third layer is different from other two layers (A) and (B), and hence, the
third layer is designated (C). If the stacking of layers is continued in
abcabcabc... pattern, then the arrangement is called cubic close packed (ccp)
structure.

13. Why ionic crystals are hard and brittle?
The
structural units of an ionic crystal are cations and anions. They are bound
together by strong electrostatic attractive forces. Cations are surrounded by
as many anions as possible and vice versa to maximize the attractive force.
14. Calculate the percentage efficiency of packing in case of body centered cubic crystal.
Packing efficiency:
The
spheres are touching along the leading diagonal of the cube
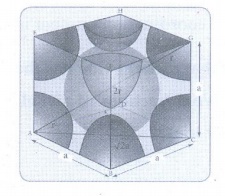
Radius
of the sphere is given as
r = √3a
/ 4
∴ Volume of the sphere with radius
'r'
=
4/3 πr3
=
4/3 π (√3/4 a)3
=
√3/16 πa3 ……………..(1)
Number
of spheres belong to a unit cell in bcc arrangement is equal to two and hence
the total volume of all spheres
=
2 × (√3πa3 / 16) = √3πa3 / 8
Formula:
Packing
fraction = [ (√3πa3 / N) /
(a3) ] × 100
=
[ √3π / 8 ] × 100
=
√3π × 12.5
=
1.732 × 3,14 × 12.5
=
68%
Packing
efficiency = 68%
Void
= 32%
15. What is the two dimensional coordination number of a molecule in square close packed layer?
In
the square close packed structure, each sphere is in contact with four of its
neighbours. The two dimensional coordination number is 4.
16. Experiment shows that Nickel oxide has the formula Ni0.96 O1.00 . What fraction of Nickel exists as of Ni2+ and Ni3+ ions?
Formula
is Ni0.96O1.00
So
the ratio of Ni : O = 96:100
So
if there are 100 atoms of oxygen then 96 atoms of Ni
Let
number of atoms of Ni2+ = x
Then
number of atoms of Ni3+ = 96−x
Charge
on Ni = charge on Oxygen
So
that oxygen has charge = −2
3(96−x)
+ 2x = 2 (100)
288
−3x + 2x = 200
−x
= −88
x
= 88
Therefore,
number of Ni2+ions = 88
And, number of Ni3+ions = 96 − 88 =
8
Fraction of nickel that exists as Ni2+
=
88/96 = 0.916
Fraction
of nickel that exists as Ni3+
=
8/96 = 0.083
Percentage
of nickel that exists as Ni2+
= 0.916 × 100 = 91.6%
Percentage
of nickel that exists as Ni3+
=
0.083 × 100 = 8.33%
17. What is meant by the term “coordination number”? What is the coordination number of atoms in a bcc structure?
• The number of nearest neighbours
that surrounding a particle in a crystal is called the coordination number of
that particle.
• In bcc structure the entire
corner atom touches the atom that occupies the body centre. Hence, each atom is
surrounded by eight nearest neighbors and coordination number is 8.
18. An element has bcc structure with a cell edge of 288 pm. the density of the element is 7.2 gcm-3. how many atoms are present in 208g of the element.
Given:
Cell
edge = 208pm ; Density = 7.2 g cm−1; n= 2
Solution:
volume
of 208g of element
mass
/ density = ( 208g ) / (7.2g cm-3 )
=
28.88 cm3
The
number of unit cell = [ 28.88 cm3
] / [ 2.39 ×10-23] cm3 / unitcell
BCC
Contains 2 atoms per unit cell
Total
number of atoms Unit cell = 2 × 12.08 × l023
Number
of atoms present = 24.16 × 1023 atoms
19. Aluminium crystallizes in a cubic close packed structure. Its metallic radius is 125pm. calculate the edge length of unit cell.
Answer:
Given:
Radius
= 125 pm; Edge length = ?
Formula: 4r = √2a
Solution:
4r
= √2a
a
=4r / √2 = 4×125 / √2 = 500/√2
Edge
length = 353.5 pm
20. if NaCl is doped with 10-2 mol percentage of strontium chloride, what is the concentration of cation vacancy?
Given:
Concentration
of SrCl2 = 10−2 mol%
Solution:
=
10−2 / 100 moles of SrCl2
=
10−4 mol of SrCl2
Concentration
is in percentage so that take total 100 mol of solution
Number
of moles of NaCl = 100 − moles of SrCl2
Moles
of SrCl2 is very negligible as compare to total moles
Number
of moles of NaCl = 100
1
mol of NaCl is doped with = 10−2/100 moles of SrCl2
=
10−4 mol of SrCl2
Cation
vacancies per mole of NaCl =10−4 mol
1
mol = 6.022 × l023 particles
Cation
vacancies per mole of NaCl
= 10−4 × 6.022 × l023 =
6.02 × l019
21. KF crystallizes in fcc structure like sodium chloride. calculate the distance between K+ and F− in KF.( given : density of KF is 2.48 g cm−3 )
Given:
n
= 4
Density
= 2.48gcm−3
M = 58.08g / mol−1
NA = 6.023 × 1023
Formula:
ρ = nM / NAa3
a 3 = nM / ρNA
Solution:
a3 = [ 4 × 58.8 ] / [ 248 × 6.023
× 1023 ]
=
[ 232.32 / 1.5×10-24] cm3
a
= 5.37 × l0−10 cm = 537 pm
Edge
length (a) = 2r
r = a / 2
537
/ 2 = 268 pm
22. An atom crystallizes in fcc crystal lattice and has a density of 10 gcm−3 with unit cell edge length of 100pm. calculate the number of atoms present in 1 g of crystal.
Answer:
Given:-
Edge
length = 100pm
Density
= l0g cm−3
n
= 4
Solution:
Volume
of unit cell = (100pm)3
=
(100 ×l0−12m)3
= (100 × 10−10cm)3
= l × l0−24cm3
Volume
of 1 g of crystal = mass / density
=
1g / 10 gcm−3 = 0.1 cm3
Number
of unit cell = [ 0.1 cm3 ]
/ [ 1 × 10−24cm3/unitcell ]
=
l × 1023 unitcell
Fcc
contains 4 atoms
Total
number of atoms for 1 g = 4 × 1 × 1023
=
4 × 1023 atoms
23. Atoms X and Y form bcc crystalline structure. Atom X is present at the corners of the cube and Y is at the centre of the cube. What is the formula of the compound?
Each
corner shared by 8 unit cells. Eight corners contributes 8/8 = 1
X=
1
Y
present at the centre of the cube.
Centre
atom shared by one unit cell. The formula of the compound is XY.
24. Sodium metal crystallizes in bcc structure with the edge length of the unit cell 4.3 ×10−8 cm . calculate the radius of sodium atom.
Given:
Na
crystallizes in bcc structure
Edge
length = 4.3 × 10−8cm
Solution:
Distance
4r = √3 a
r
= √3/4 × 4.3 × 10−8
=
7.44 / 4 × 10−8
=
1.86 × 10−8 cm
Radius
of Na atom = 1.86 × 10−8 cm
= 1.86 Ǻ
=
186 pm
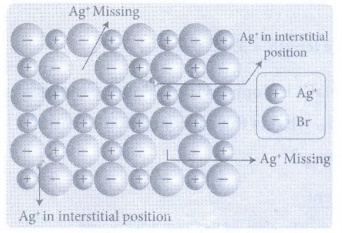
25. Write a note on Frenkel defect.
Frenkel
defect arises due to the dislocation of ions from its crystal lattice. The
missing ion occupies an interstitial position. This defect is shown by ionic
solids in which cation and anion differ in size. This defect does not affect
the density of the crystal.
For
example, In AgBr, small Ag+ ion leaves its normal site and occupies
an interstitial position
EVALUATE YOURSELF:
1. An element has a
face centered cubic unit cell with a length of 352.4 pm along an edge. The density
of the element is 8.9 g cm−3. How many atoms are present in 100 g of
an element?
Given:
Density:
8.9 g cm−3
a
= 352.4 pm = 3.524 × l0−8 cm, Mass = 100g, Z = 4
M
= [ a3ρ × NA ] / n
=
[ (3.524 × 10−8)3 × 8.9 × 6.023 × 1023 ] / 4
=
[ 2345.9 × 10−1 ] / 4 = 586.5 × 10−1 = 58.65 gmol−1
Number
of atoms of an element
=
( mass / atomic mass ) × 6.023 × 1023
Number
of atoms in l00g of an element
=
[100/58.65] × 6.023 × 1023 = 10.27 × 1023 atoms
2. Determine the
density of CsCl which crystallizes in a bcc type structure with an edge length
412.1 pm.
Given:
M
= 133 + 35.5 = 168.5 g mol−1,
a
= 412.1 pm = 4.121 × 10−8 cm, Z = 1
ρ = ( M × n )/ ( a3 × NA
) = [ 168.5 × 1 ] / { (4.121 × 10−8)3 × 6.023 × 1023
} = 168.5 / 42.15 = 3.99
Density
of CsCl crystal = 4 g cm−3
3. A face centered
cubic solid of an element (atomic mass 60) has a cube edge of 4A. Calculate its
density.
Given:
M
= 60 g mol−1 ; a = 4Ǻ = 4 × 10−8 cm, Z = 4
ρ = [M × n
] / [ a3 × N A
] = [ 60 × 4] / [ (4 × l0−8)3 × 6.023 × 1023 ]
=
240 / 38.54 = 6.227 g cm−3
Density
of an element = 6.227 g cm−3
4. Barium has a
body centered cubic unit cell with a length of 508 pm along an edge. What is
the density of barium in g cm−3?
Given:
M
= 137.3 g mol−1, a = 508 pm = 5.08 × 10−8 cm,
Z = 2
ρ
= [ M × n ] / [ a3 × NA ]
=
[ 137.3 × 2 ] / [ (5.08 × 10−8)3 × 6.023 × 1023 ]
= 274.6 / 78. 96 = 3.478 g cm−3 = 3.5 g cm−3

Related Topics