Packing in crystals

Packing in crystals:

Let us consider the packing of fruits for display in fruit stalls. They are in a closest packed arrangement as shown in the following fig. we can extend this analogy to visualize the packing of constituents (atoms / ions / molecules) in crystals, by treating them as hard spheres. To maximize the attractive forces between the constituents, they generally tend to pack together as close as possible to each other. In this portion we discuss how to pack identical spheres to create cubic and hexagonal unit cell. Before moving on to these three dimensional arrangements, let us first consider the two dimensional arrangement of spheres for better understanding.

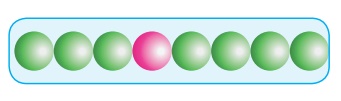
1. Linear arrangement of spheres in one direction:

In a specific direction, there is only one possibility to arrange the spheres in one direction as shown in the fig. in this arrangement each sphere is in contact with two neighbouring spheres on either side.

2. Two dimensional close packing:

Two dimensional planar packing can be done in the following two different ways.

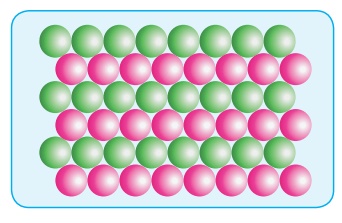
(i) AAA… type:

Linear arrangement of spheres in one direction is repeated in two dimension i.e., more number of rows can be generated identical to the one dimensional arrangement such that all spheres of different rows align vertically as well as horizontally as shown in the fig. If we denote the first row as A type arrangement, then the above mentioned packing is called AAA type, because all rows are identical as the first one. In this arrangement each sphere is in contact with four of its neighbours.

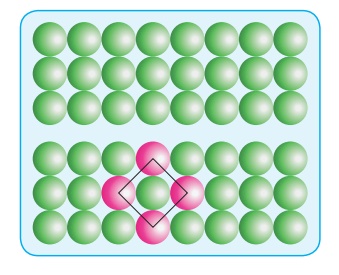
(i) ABAB.. Type:

In this type, the second row spheres are arranged in such a way that they fit in the depression of the first row as shown in the figure. The second row is denoted as B type.

The third row is arranged similar to the first row A, and the fourth one is arranged similar to second one. i.e., the pattern is repeated as ABAB….In this arrangement each sphere is in contact with 6 of its neighbouring spheres.

On comparing these two arrangements (AAAA...type and ABAB….type) we found that the closest arrangement is ABAB…type.

3. Simple cubic arrangement:

This type of three dimensional packing arrangements can be obtained by repeating the type two dimensional arrangements in three dimensions. i.e., spheres in one layer sitting directly on the top of those in the previous layer so that all layers are identical. All spheres of different layers of crystal are perfectly aligned horizontally and also vertically, so that any unit cell of such arrangement as simple cubic structure as shown in fig.

In simple cubic packing, each sphere is in contact with 6 neighbouring spheres - Four in its own layer, one above and one below and hence the coordination number of the sphere in simple cubic arrangement is 6.

Packing efficiency:

There is some free space between the spheres of a single layer and the spheres of successive layers. The percentage of total volume occupied by these constituent spheres gives the packing efficiency of an arrangement. Let us calculate the packing efficiency in simple cubic arrangement,

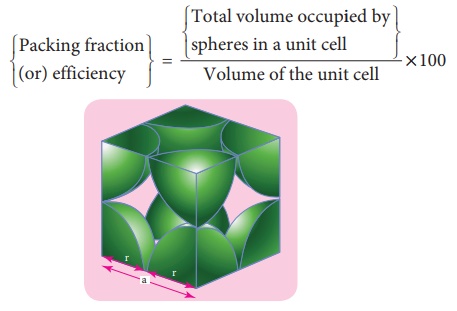
Let us consider a cube with an edge length ‘a’ as shown in fig. Volume of the cube with edge length a is = a × a × a = a³

Let ‘r’ is the radius of the sphere. From the figure, a=2r ⇒ r = a/2

∴ Volume of the sphere with radius ‘r’

In a simple cubic arrangement, number of spheres belongs to a unit cell is equal to one

i.e., only 52.31% of the available volume is occupied by the spheres in simple cubic packing, making inefficient use of available space and hence minimizing the attractive forces.

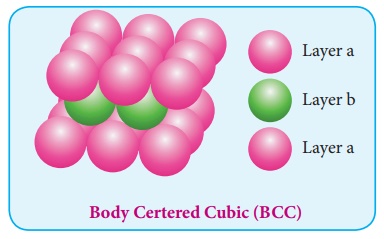
4. Body centered cubic arrangement

In this arrangement, the spheres in the first layer ( A type ) are slightly separated and the second layer is formed by arranging the spheres in the depressions between the spheres in layer A as shown in figure. The third layer is a repeat of the first. This pattern ABABAB is repeated throughout the crystal. In this arrangement, each sphere has a coordination number of 8, four neighbors in the layer above and four in the layer below.

Packing efficiency:

Here, the spheres are touching along the leading diagonal of the cube as shown in the fig.

Number of spheres belong to a unit cell in bcc arrangement is equal to two and hence the total volume of all spheres

i.e., 68 % of the available volume is occupied. The available space is used more efficiently than in simple cubic packing.

5. The hexagonal and face centered cubic arrangement:

Formation of first layer:

In this arrangement, the first layer is formed by arranging the spheres as in the case of two dimensional ABAB arrangements i.e. the spheres of second row fit into the depression of first row. Now designate this first layer as ‘a’. The next layer is formed by placing the spheres in the depressions of the first layer. Let the second layer be ‘b’.

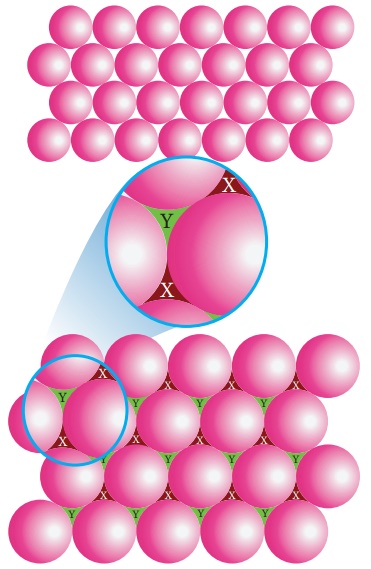
Formation of second layer:

In the first layer (a) there are two types of voids (or holes) and they are designated as x and y. The second layer can be formed by placing the spheres either on the depression (voids/holes) x (or) on y. let us consider the formation of second layer by placing the spheres on the depression (x).

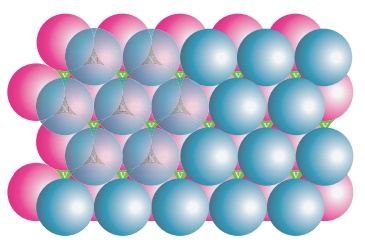
Wherever a sphere of second layer is above the void (x) of the first layer (a), a tetrahedral void is formed. This constitutes four spheres – three in the lower (a) and one in the upper layer (b). When the centers of these four spheres are joined, a tetrahedron is formed.

At the same time, the voids (y) in the first layer (a) are partially covered by the spheres of layer (b), now such a void in (a) is called a octahedral void. This constitutes six spheres – three in the lower layer (a) and three in the upper layer (b). When the centers of these six spheres are joined, an octahedron is formed. Simultaneously new tetrahedral voids (or holes) are also created by three spheres in second layer (b) and one sphere of first layer (a)

 Formation of third layer:

The third layer of spheres can be formed in two ways to achieve closest packing

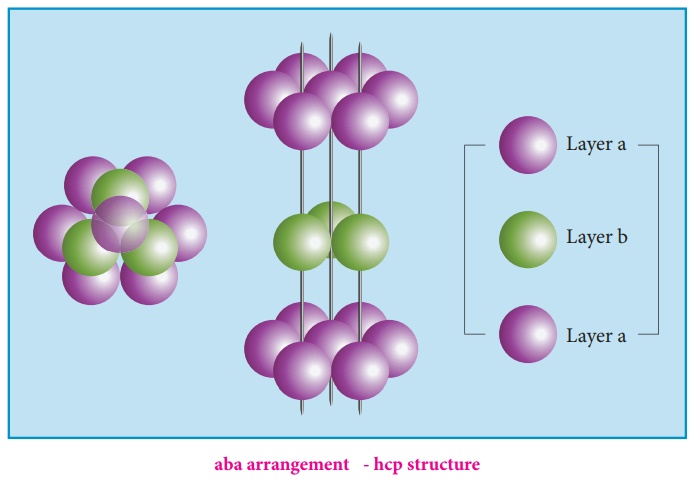
(i) aba arrangement - hcp structure

(ii) abc arrangement – ccp structure

The spheres can be arranged so as to fit into the depression in such a way that the third layer is directly over a first layer as shown in the figure. This “aba’’ arrangement is known as the hexagonal close packed (hcp) arrangement. In this arrangement, the tetrahedral voids of the second layer are covered by the spheres of the third layer.

Alternatively, the third layer may be placed over the second layer in such a way that all the spheres of the third layer fit in octahedral voids. This arrangement of the third layer is different from other two layers (a) and (b), and hence, the third layer is designated (c). If the stacking of layers is continued in abcabcabc… pattern, then the arrangement is called cubic close packed (ccp) structure.

In both hcp and ccp arrangements, the coordination number of each sphere is 12 – six neighbouring spheres in its own layer, three spheres in the layer above and three sphere in the layer below. This is the most efficient packing.

The cubic close packing is based on the face centered cubic unit cell. Let us calculate the packing efficiency in fcc unit cell.

Total number of spheres belongs to a single fcc unit cell is 4

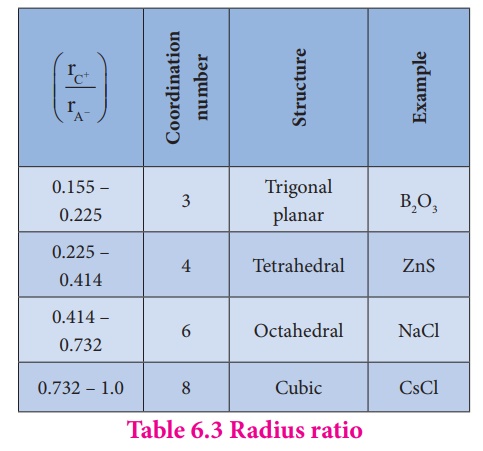
Radius ratio:

The structure of an ionic compound depends upon the stoichiometry and the size of the ions.generally in ionic crystals the bigger anions are present in the close packed arrangements and the cations occupy the voids. The ratio of radius of cation and anion (r_C/r_A) plays an important role in determining the structure. The following table shows the relation between the radius ratio and the structural arrangement in ionic solids.