Scheduling Techniques: Critical Path Method

Scheduling Techniques

Scheduling is one of the areas that received considerable attention from researchers as well as practitioners in all types of applications including operations scheduling and project scheduling. Techniques are developed to develop optimum or near optimal schedules with respect to different possible performance measures. This chapter highlights some of these techniques and their application in maintenance scheduling.

Critical Path Method

To  identify  the  critical  path  using  the  CPM  method  we  need  to  follow  the following steps:

1.   Develop the project network diagram as shown in the previous section;

2.  Perform the CPM calculation to identify the critical jobs (there are jobs on the critical paths and non-critical jobs (which are jobs with float);

3.   Perform  project  crashing  to  (determine  minimum  times  for  each  job)

reduce project duration and investigate the cost tradeoffs; and

4. Level the resources in order to have uniform manpower requirements to minimize hiring, firing, or overtime requirements.

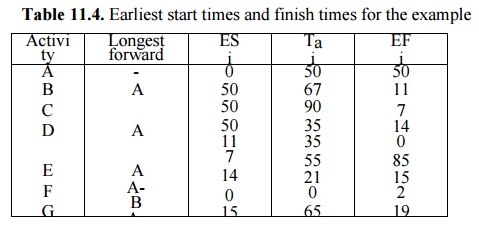
The critical path calculation includes two phases. The first phase is the forward pass (starting with the first node and proceeding to the last node). In this phase, the earliest start time, ES, and earliest finish time, EF, are determined for each activity. The earliest start time ESi for a given activity, i, is the earliest possible time in the schedule that activity i can be started. Its value is determined by summing up the activity times of the activities lying on the longest path leading to it. The earliest finish time EFi for a given activity i, is its earliest start time plus its activity time  Tai. The calculations for the bearing overhaul example are shown in Table 11.4.

Table 11.4. Earliest start times and finish times for the example

The second phase is the backward pass (starting with the last node and proceeding back to the first node). We start this phase by assuming that the total project time Tcp, is the earliest finish time, EF, of the last activity found in the forward pass. In this phase, the latest finish time, LF, and latest start time, LS, are determined for each activity. The latest finish time LFi for a given activity, i, is the latest possible time that activity i must be completed in order to finish the whole project on schedule. Its value is determined by subtracting from Tcp the activity time along the longest path leading backward from the last node. For the last activity of the schedule, LF is set to be the total time duration of the project, Tcp. The latest finish time, LFi , for a given activity, i, is its latest finish time minus its activity time Tai. The calculations for the bearing overhaul example are shown in Table 11.5.

Table 11.5. Latest finish times and start times for the example

The last step in the analysis of the network is to determine the slack time for each activity Si. It can be determined by the difference between the latest and the earliest start time of the activity. The calculations are shown in Table 11.6 below.

Table 11.6. Slack times for the example

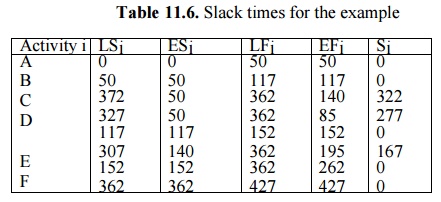
Note that the activities along the critical path (A-B-E-G-H-I) have zero slack times. Activities not lying on the critical path have positive slacks, meaning that they could be delayed by an amount of time equal to their slack without delaying the project completion time.

The construction of the time chart should be made taking into consideration the available resources, and must take full advantage of the CPM calculation. In some circumstances it might not be possible to schedule many activities simultaneously because of personnel and equipment limitations. The total float for non-critical activities can be used to level the resources and minimize the maximum resource requirement. These activities can be shifted backward and forward between maximum allowable limits and scheduled at an appropriate time that levels the resources and keeps a steady workforce and equipment.

In addition to resource leveling, CPM involves project crashing. In project crashing, the duration of one or more critical activities are shortened in an optimal fashion and a curve is prepared to show the trade off between time and cost. This will enable management to evaluate project duration with the resulting cost. Network programming can be used to perform crashing in an optimal fashion. For more on project scheduling, see Taha (1992).