Pharmacokinetics: Compartment Models

Compartment Models

Multicompartment models provide a mathemati-cal framework that can be used to relate drug dose to changes in drug concentrations over time. Conceptually, the compartments in these models are tissues with a similar distribution time course. For example, the plasma and lungs are components of the central compartment. The organs and muscles, sometimes called the vessel-rich group, could be the second, or rapidly equilibrating, compartment. Fat and skin have the capacity to bind large quan-tities of lipophilic drug but are poorly perfused. These could represent the third, or slowly equili-brating, compartment. This is an intuitive definition of compartments, and it is important to recognize that the compartments of a pharmacokinetic model are mathematical abstractions that relate dose to observed concentration. A one-to-one relationship does not exist between any compartment and any organ or tissue in the body.

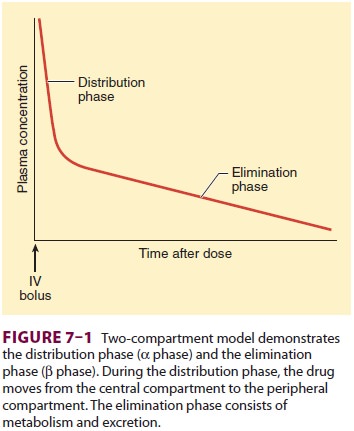
Many drugs used in anesthesia are well described by a two-compartment model. This is generally the case if the studies used to characterize the pharmacokinetics do not include rapid arterial sampling over the first few minutes (Figure 7–1). Without rapid arterial sampling the ultra-rapid ini-tial drop in plasma concentration immediately after a bolus injection is missed, and the central compart-ment volume is blended into the rapidly equilibrat-ing compartment. When rapid arterial sampling is used in pharmacokinetic experiments, the results are generally a three-compartment model. In these cases the number of identifiable compartments is a function of the experimental design and not a char-acteristic of the drug.

In compartmental models the instantaneous concentration at the time of a bolus injection is assumed to be the amount of the bolus divided by the central compartment volume. This is not

correct. If the bolus is given over a few seconds, the instantaneous concentration is 0, because the drug is all in the vein, still flowing to the heart. It takes only a minute or two for the drug to mix in the cen-tral compartment volume. This misspecification is common to conventional pharmacokinetic mod-els. More physiologically based models, sometimes called front-end kinetic models, can characterize the initial delay in concentration. These models are useful only if the concentrations over the first few minutes are clinically important. After the first few minutes, front-end models resemble conventional compartmental models.

In the first few minutes following initial bolus administration of a drug, the concentration drops very rapidly as the drug quickly diffuses into periph-eral compartments. The decline is typically an order of magnitude over 10 minutes. For drugs with very rapid hepatic clearance (eg, propofol) or those that are metabolized in the blood (eg, remifentanil), metabolism contributes significantly to the rapid ini-tial drop in concentration. Following this very rapid drop there is a period of slower decrease in plasma concentration. During this period, the rapidly equilibrating compartment is no longer removing drug from the plasma. Instead, drug returns to the plasma from the rapidly equilibrating compartment. The reversed role of the rapidly equilibrating tissues from extracting drug to returning drug accounts for the slower rate of decline in plasma concentration in this intermediate phase. Eventually there is an even slower rate of decrease in plasma concentration, which is log-linear until the drug is completely elim-inated from the body. This terminal log-linear phase occurs after the slowly equilibrating compartment shifts from net removal of drug from the plasma to net return of drug to the plasma. During this ter-minal phase the organ of elimination (typically the liver) is exposed to the body’s entire body drug load, which accounts for the very slow rate of decrease in plasma drug concentration during this final phase.

The mathematical models used to describe a drug with two or three compartments are, respectively:

Cp(t) = Ae^−αt+ Be^−βt

and

Cp(t) = Ae^−αt+ Be^−βt+ Ce^−γt

where Cp(t) equals plasma concentration at time t, and α, β, and γ are the exponents that character-ize the very rapid (ie, very steep), intermediate, and slow (ie, log-linear) portions of the plasma concen-tration over time, respectively. Drugs described by two-compartment and three-compartment models will have two or three half-lives. Each half-life is cal-culated as the natural log of 2 (0.693), divided by the exponent. The coefficients A, B, and C represent the contribution of each of the exponents to the overall decrease in concentration over time.

The two-compartment model is described by a curve with two exponents and two coefficients, whereas the three-compartment model is described by a curve with three exponents and three coeffi-cients. The mathematical relationships among com-partments, clearances, coefficients, and exponents are complex. Every coefficient and every exponent is a function of every volume and every clearance.

Elimination half-life is the time required for the drug concentration to fall by 50%. For drugsdescribed by multicompartment pharmacokinetics (eg, all drugs used in anesthesia), there are multiple elimination half-lives, in other words the elimination half-time is context dependent. The offset of a drug’s effect cannot be predicted from half-lives. Moreover, one cannot easily determine how rapidly a drug effect will disappear simply by looking at coefficients, exponents, and half-lives. For example, the terminal half-life of sufentanil is about 10 h, whereas that of alfentanil is 2 h. This does not mean that recovery from alfentanil will be faster, because clinical recovery from clinical dosing will be influ-enced by all half-lives, not just the terminal one. Computer models readily demonstrate that recovery from an infusion lasting several hours will be faster when the drug administered is sufentanil than it will be when the infused drug is alfentanil. The time required for a 50% decrease in concentration depends on the duration or “context” of the infusion. The con-text-sensitive half-time, discussed earlier, captures this concept and should be used instead of half-lives to compare the pharmacokinetic properties of intra-venous drugs used in anesthesia.