Pharmacodynamics

PHARMACODYNAMICS

Pharmacodynamics, the study of how drugs affect the body, involves the concepts of potency, efficacy, and therapeutic window. Pharmacokinetic mod-els can range from entirely empirical dose versus response relationships to mechanistic models of ligand–receptor binding. The fundamental pharma-codynamic concepts are captured in the relation-ship between exposure to a drug and physiological response to the drug, often called the dose–response or concentration–response relationship.

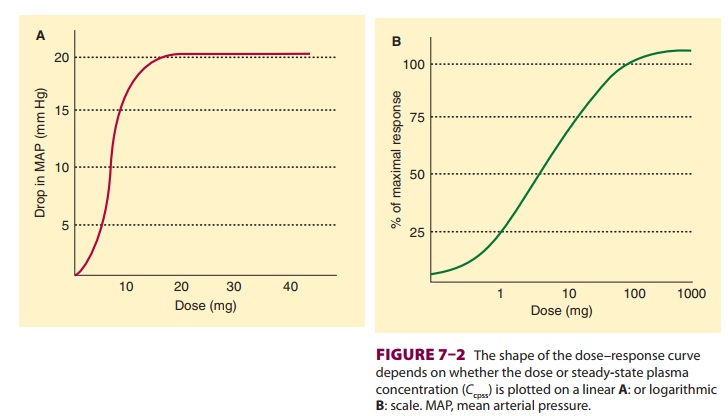
Exposure–Response Relationships

As the body is exposed to an increasing amount of a drug, the response to the drug similarly increases, typically up to a maximal value. This fundamental concept in the exposure versus response relationship is captured graphically by plotting exposure (usually dose or concentration) on the x axis as the indepen-dent variable, and the body’s response on the y axis as the dependent variable. Depending on the cir-cumstances, the dose or concentration may be plot-ted on a linear scale (Figure 7–2A) or a logarithmic

scale ( Figure 7–2B), while the response is typi-cally plotted either as the actual measured response (Figure 7–2A) or as a fraction of the baseline or max-imum physiological measurement (Figure 7–2B). For our purposes here, basic pharmacodynamic properties are described in terms of concentration, but any metric of drug exposure (dose, area under the curve, etc) could be used.

The shape of the relationship is typically sig-moidal, as shown in Figure 7–2. The sigmoidal

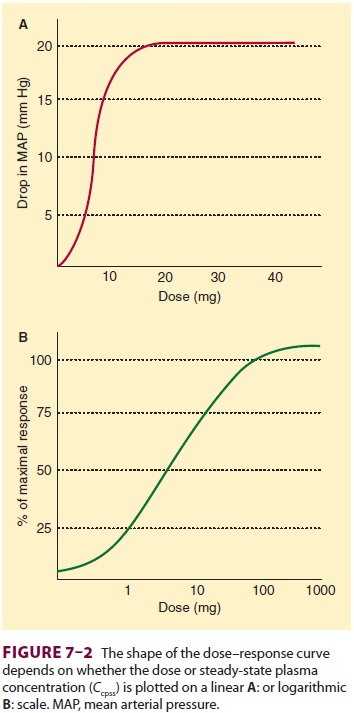
shape reflects the observation that often a certain amount of drug must be present before there is any measurable physiological response. Thus, the left side of the curve is flat until the drug concentration reaches a minimum threshold. The right side is also flat, reflecting the maximum physiological response of the body, beyond which the body simply cannot respond to additional drug (with the possible excep-tion of eating and weight). Thus, the curve is flat on both the left and right sides. A sigmoidal curve is required to connect the baseline to the asymptote, which is why sigmoidal curves are ubiquitous when modeling pharmacodynamics

The sigmoidal relationship between exposure and response is defined by one of two interchange-able relationships:

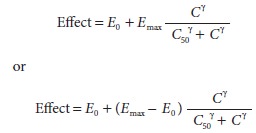
In both cases, E₀ is the baseline effect in the absence of drug, C is drug concentration, C₅₀ is the concentration associated with half-maximal effect, and γ describes the steepness of the concentration ver-sus response relationship. For the first equation, E_max is the maximum change from baseline. In the second equation, E_max is the maximum physiological mea-surement, not the maximum change from baseline.

Once defined in this fashion, each parameter of the pharmacodynamic model speaks to the spe-cific concepts mentioned earlier. E_max is related to the intrinsic efficacy of a drug. Highly efficacious drugs have a large maximum physiological effect, characterized by a large E_max. For drugs that lack efficacy, E_max will equal E₀. C₅₀ is a measure of drug potency. Highly potent drugs have a low C₅₀; thus small amounts produce the drug effect. Drugs lack-ing potency have a high C₅₀, indicating that a large amount of drug is required to achieve the drug effect. The parameter γ indicates steepness of the relationship between concentration and effect. A γ value less than 1 indicates a very gradual increase in drug effect with increasing concentration. A value greater than 4 suggests that once drug effect is observed, small increases in drug concentration produce large increases in drug effect until the maxi-mum effect is reached.

The curve described above represents the rela-tionship of drug concentration to a continuous physiological response. The same relationship can be used to characterize the probability of a binary (yes/no) response to a drug dose:

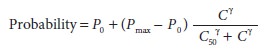
In this case, the probability (P) ranges from 0 (no chance) to 1 (certainty). P₀ is the probability of a “yes” response in the absence of drug. P_max is the maximum probability, necessarily less than or equal to 1. As before, C is the concentration, C₅₀ is the concentration associated with half-maximal effect, and γ describes the steepness of the concentration versus response relationship. Half-maximal effect is the same as 50% probability of a response when P₀ is 0 and P_max is 1.

The therapeutic window for a drug is the range between the concentration associated with a desired therapeutic effect and the concentration associated with a toxic drug response. This range can be mea-sured either between two different points on the same concentration versus response curve, or the distance between two distinct curves. For a drug such as sodium nitroprusside, a single concentra-tion versus response curve defines the relationship between concentration and decrease in blood pres-sure. The therapeutic window might be the differ-ence in the concentration producing a desired 20% decrease in blood pressure and a toxic concentration that produces a 60% decrease in blood pressure. However, for a drug such as lidocaine, the thera-peutic window might be the difference between the C₅₀for local anesthesia and the C₅₀for lidocaine-induced seizures, the latter being a separate concen-tration versus response relationship. The therapeutic index is the C₅₀ for toxicity divided by the C₅₀ for the desired therapeutic effect. Because of the risk of ventilatory and cardiovascular depression (even at concentrations only slightly greater than those pro-ducing anesthesia), most inhaled and intravenous hypnotics are considered to have very low therapeu-tic indices relative to other drugs.

Drug Receptors

Drug receptors are macromolecules, typically pro-teins, that bind a drug (agonist) and mediate the drug response. Pharmacological antagonists reverse the effects of the agonist but do not otherwise exert an effect of their own. Competitive antagonism occurs when the antagonist competes with the agonist for the binding site, each potentially displacing the other. Noncompetitive antagonism occurs when the antag-onist, through covalent binding or another process, permanently impairs the drug’s access to the receptor.

The drug effect is governed by the fraction of receptors that are occupied by an agonist. That frac-tion is based on the concentration of the drug, the concentration of the receptor, and the strength of binding between the drug and the receptor. This binding is described by the law of mass action, which states that the reaction rate is proportional to the concentrations of the reactants:

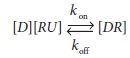
where [D] is the concentration of the drug, [ RU] is the concentration of unbound receptor, and [DR] is the concentration of bound receptor. The rate con-stant k_on defines the rate of ligand binding to the receptor. The rate constant k_off defines the rate of ligand unbiom the receptor. According to the law of mass action, the rate of receptor binding, d[DR]/dt is:nding fr

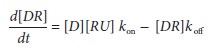
Steady state occurs almost instantly. Because the rate of formation at steady state is 0, it follows that:

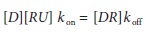
In this equation, k_d is the dissociation rate con-stant, defined as k_on/k_off. If we define f, fractional receptor occupancy, as:

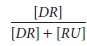
then we can solve for receptor occupancy as:

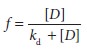
The receptors are half occupied when [ D] =k_d. Thus, k_d is the concentration of drug associated with 50% receptor occupancy.

Receptor occupancy is only the first step in mediating drug effect. Binding of the drug to the receptor can trigger a myriad of subsequent steps, including opening or closing of an ion channel, activation of a G protein, activation of an intracel-lular kinase, direct interaction with a cellular struc-ture, or direct binding to DNA.

Like the concentration versus response curve, the shape of the curve relating fractional receptor occupancy to drug concentration is intrinsically sigmoidal. However, the concentration associated with 50% receptor occupancy and the concentra-tion associated with 50% of maximal drug effect are not necessarily the same. Maximal drug effect could occur at very low receptor occupancy, or (for partial agonists) at greater than 100% receptor occupancy.

Prolonged binding and activation of a receptor by an agonist may lead to hyporeactivity (“desensi-tization”) and tolerance. If the binding of an endog-enous ligand is chronically blocked, then receptors may proliferate resulting in hyperreactivity and increased sensitivity.