Performance of the MPI solvers

Performance of the MPI solvers

Table 6.5 shows the run-times of the two n-body solvers when they’re run with 800 particles for 1000 timesteps on an Infiniband-connected cluster. All the timings were taken with one process per cluster node. The run-times of the serial solvers differed from the single-process MPI solvers by less than 1%, so we haven’t included them.

Clearly, the performance of the reduced solver is much superior to the perfor-mance of the basic solver, although the basic solver achieves higher efficiencies.

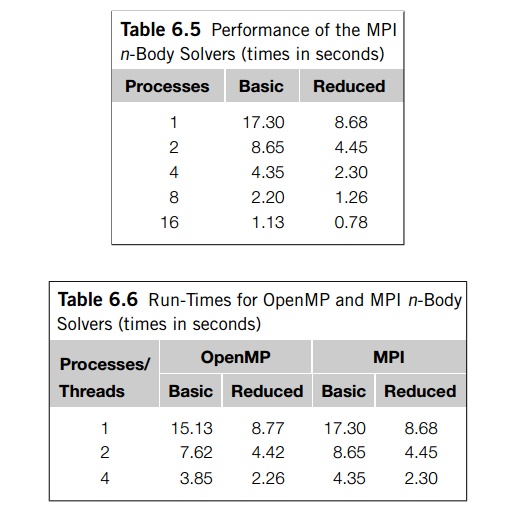
For example, the efficiency of the basic solver on 16 nodes is about 0.95, while the efficiency of the reduced solver on 16 nodes is only about 0.70.

A point to stress here is that the reduced MPI solver makes much more efficient use of memory than the basic MPI solver; the basic solver must provide storage for all n positions on each process, while the reduced solver only needs extra storage for n/comm._sz positions and n/comm._sz forces. Thus, the extra storage needed on each process for the basic solver is nearly comm._sz=2 times greater than the storage needed for the reduced solver. When n and comm._sz are very large, this factor can easily make the difference between being able to run a simulation only using the process’ main memory and having to use secondary storage.

The nodes of the cluster on which we took the timings have four cores, so we can compare the performance of the OpenMP implementations with the performance of the MPI implementations (see Table 6.6). We see that the basic OpenMP solver is a good deal faster than the basic MPI solver. This isn’t surprising since MPI_Allgather is such an expensive operation. Perhaps surprisingly, though, the reduced MPI solver is quite competitive with the reduced OpenMP solver.

Let’s take a brief look at the amount of memory required by the MPI and OpenMP reduced solvers. Say that there are n particles and p threads or processes. Then each solver will allocate the same amount of storage for the local velocities and the local positions. The MPI solver allocates n doubles per process for the masses. It also allocates 4n/p doubles for the tmp_pos and tmp_forces arrays, so in addition to the local velocities and positions, the MPI solver stores

n + 4n/p

doubles per process. The OpenMP solver allocates a total of 2pn + 2n doubles for the forces and n doubles for the masses, so in addition to the local velocities and positions, the OpenMP solver stores

3n/p + 2n

doubles per thread. Thus, the difference in the local storage required for the OpenMP version and the MPI version is

n-n/p

doubles. In other words, if n is large, the local storage required for the MPI ver-sion is substantially less than the local storage required for the OpenMP version. So, for a fixed number of processes or threads, we should be able to run much larger simulations with the MPI version than the OpenMP version. Of course, because of hardware considerations, we’re likely to be able to use many more MPI processes than OpenMP threads, so the size of the largest possible MPI simulations should be much greater than the size of the largest possible OpenMP simulations. The MPI ver-sion of the reduced solver is much more scalable than any of the other versions, and the “ring pass” algorithm provides a genuine breakthrough in the design of n-body solvers.