Evaluating the OpenMP codes

Evaluating the OpenMP codes

Before we can compare the basic and the reduced codes, we need to decide how to schedule the parallelized for loops. For the basic code, we’ve seen that any schedule that divides the iterations equally among the threads should do a good job of balanc-ing the computational load. (As usual, we’re assuming no more than one thread/core.) We also observed that a block partitioning of the iterations would result in fewer cache misses than a cyclic partition. Thus, we would expect that a block schedule would be the best option for the basic version.

In the reduced code, the amount of work done in the first phase of the computation of the forces decreases as the for loop proceeds. We’ve seen that a cyclic schedule should do a better job of assigning more or less equal amounts of work to each thread. In the remaining parallel for loops—the initialization of the loc forces array, the second phase of the computation of the forces, and the updating of the positions and velocities—the work required is roughly the same for all the iterations. Therefore, taken out of context each of these loops will probably perform best with a block schedule. However, the schedule of one loop can affect the performance of another (see Exercise 6.10), so it may be that choosing a cyclic schedule for one loop and block schedules for the others will degrade performance.

With these choices, Table 6.3 shows the performance of the n-body solvers when they’re run on one of our systems with no I/O. The solver used 400 particles for 1000 timesteps. The column labeled “Default Sched” gives times for the OpenMP reduced solver when all of the inner loops use the default schedule, which, on our system, is a block schedule. The column labeled “Forces Cyclic” gives times when the first phase of the forces computation uses a cyclic schedule and the other inner loops use the default schedule. The last column, labeled “All Cyclic,” gives times when all of

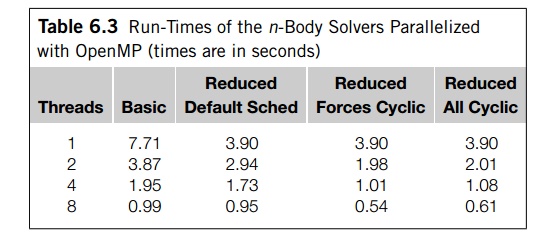
the inner loops use a cyclic schedule. The run-times of the serial solvers differ from those of the single-threaded solvers by less than 1%, so we’ve omitted them from the table.

Notice that with more than one thread the reduced solver, using all default sched-ules, takes anywhere from 50 to 75% longer than the reduced solver with the cyclic forces computation. Using the cyclic schedule is clearly superior to the default sched-ule in this case, and any loss in time resulting from cache issues is more than made up for by the improved load balance for the computations.

For only two threads there is very little difference between the performance of the reduced solver with only the first forces loop cyclic and the reduced solver with all loops cyclic. However, as we increase the number of threads, the performance of the reduced solver that uses a cyclic schedule for all of the loops does start to degrade. In this particular case, when there are more threads, it appears that the overhead involved in changing distributions is less than the overhead incurred from false sharing.

Finally, notice that the basic solver takes about twice as long as the reduced solver with the cyclic scheduling of the forces computation. So if the extra memory is avail-able, the reduced solver is clearly superior. However, the reduced solver increases the memory requirement for the storage of the forces by a factor of thread count, so for very large numbers of particles, it may be impossible to use the reduced solver.