A dynamic parallelization of tree search using pthreads

A dynamic parallelization of tree search using pthreads

If the initial distribution of subtrees doesn’t do a good job of distributing the work among the threads, the static parallelization provides no means of redistributing work. The threads with “small” subtrees will finish early, while the threads with large sub-trees will continue to work. It’s not difficult to imagine that one thread gets the lion’s share of the work because the edges in its initial tours are very cheap, while the edges in the other threads’ initial tours are very expensive. To address this issue, we can try to dynamically redistribute the work as the computation proceeds.

To do this, we can replace the test !Empty(my_stack) controlling execution of the while loop with more complex code. The basic idea is that when a thread runs out of work—that is, !Empty(my_stack) becomes false instead of immediately exiting the while loop, the thread waits to see if another thread can provide more work. On the other hand, if a thread that still has work in its stack finds that there is at least one thread without work, and its stack has at least two tours, it can “split” its stack and provide work for one of the threads.

Pthreads condition variables provide a natural way to implement this. When a thread runs out of work it can call pthread_cond_wait and go to sleep. When a thread with work finds that there is at least one thread waiting for work, after splitting its stack, it can call pthread_cond_signal. When a thread is awakened it can take one of the halves of the split stack and return to work.

This idea can be extended to handle termination. If we maintain a count of the number of threads that are in pthread_cond_wait, then when a thread whose stack is empty finds that thread_count-1 threads are already waiting, it can call pthread_cond_broadcast and as the threads awaken, they’ll see that all the threads have run out of work and quit

Termination

Thus, we can use the pseudocode shown in Program 6.8 for a Terminated function that would be used instead of Empty for the while loop implementing tree search.

There are several details that we should look at more closely. Notice that the code executed by a thread before it splits its stack is fairly complicated. In Lines 1–2 the thread

. checks that it has at least two tours in its stack,

. checks that there are threads waiting, and

. checks whether the new stack variable is NULL.

The reason for the check that the thread has enough work should be clear: if there are fewer than two records on the thread’s stack, “splitting” the stack will either do nothing or result in the active thread’s trading places with one of the waiting threads.

It should also be clear that there’s no point in splitting the stack if there aren’t any threads waiting for work. Finally, if some thread has already split its stack, but a waiting thread hasn’t retrieved the new stack, that is, new_stack != NULL, then it would be disastrous to split a stack and overwrite the existing new_stack. Note that this makes it essential that after a thread retrieves new_stack by, say, copying new stack into its private my_stack variable, the thread must set new_stack to NULL.

If all three of these conditions hold, then we can try splitting our stack. We can acquire the mutex that protects access to the objects controlling termination (threads_in_cond_wait, new_stack, and the condition variable). However, the condition threads in cond wait > 0 && new stack == NULL

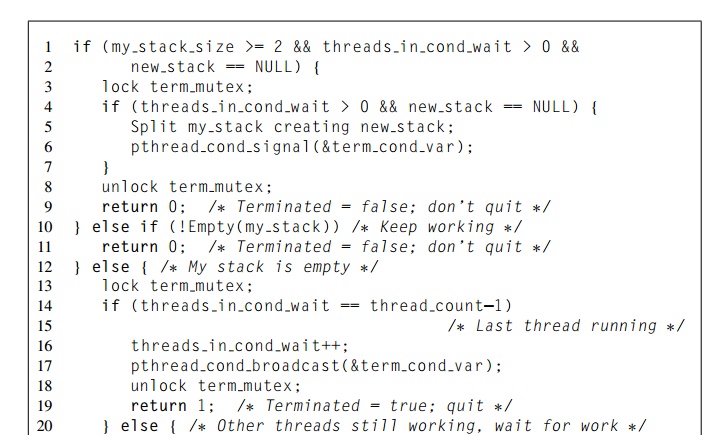
can change between the time we start waiting for the mutex and the time we actually acquire it, so as with Update_best_tour, we need to confirm that this condition is still true after acquiring the mutex (Line 4). Once we’ve verified that these conditions still hold, we can split the stack, awaken one of the waiting threads, unlock the mutex, and return to work.

If the test in Lines 1 and 2 is false, we can check to see if we have any work at all—that is, our stack is nonempty. If it is, we return to work. If it isn’t, we’ll start the termination sequence by waiting for and acquiring the termination mutex in Line 13. Once we’ve acquired the mutex, there are two possibilities:

. We’re the last thread to enter the termination sequence, that is,

. threads_in_cond_wait == thread_count-1.

Other threads are still working.

In the first case, we know that since all the other threads have run out of work, and we have also run out of work, the tree search should terminate. We therefore sig-nal all the other threads by calling pthread_cond_broadcast and returning true. Before executing the broadcast, we increment threads_in_cond_wait, even though the broadcast is telling all the threads to return from the condition wait. The reason is that threads_in_cond_wait is serving a dual purpose: When it’s less than thread_count, it tells us how many threads are waiting. However, when it’s equal to thread_count, it tells us that all the threads are out of work, and it’s time to quit.

In the second case—other threads are still working—we call pthread cond wait (Line 22) and wait to be awakened. Recall that it’s possible that a thread could be awakened by some event other than a call to pthread_cond_signal or pthread_cond_broadcast. So, as usual, we put the call to pthread_cond_wait in a while loop, which will immediately call pthread_cond_wait again if some other event (return value not 0) awakens the thread.

Once we’ve been awakened, there are also two cases to consider:

threads_in_cond_wait < thread_count

threads_in_cond_wait == thread_count

In the first case, we know that some other thread has split its stack and created more work. We therefore copy the newly created stack into our private stack, set the new_stack variable to NULL, and decrement threads_in_cond_wait (i.e., Lines 25–27). Recall that when a thread returns from a condition wait, it obtains the mutex associated with the condition variable, so before returning, we also unlock the mutex (i.e., Line 28). In the second case, there’s no work left, so we unlock the mutex and return true.

In the actual code, we found it convenient to group the termination variables together into a single struct. Thus, we defined something like

and we defined a couple of functions, one for initializing the term variable and one for destroying/freeing the variable and its members.

Before discussing the function that splits the stack, note that it’s possible that a thread with work can spend a lot of time waiting for term_mutex before being able to split its stack. Other threads may be either trying to split their stacks, or prepar-ing for the condition wait. If we suspect that this is a problem, Pthreads provides a nonblocking alternative to pthread_mutex lock called pthread_mutex_trylock

This function attempts to acquire mutex_p. However, if it’s locked, instead of waiting, it returns immediately. The return value will be zero if the calling thread has successfully acquired the mutex, and nonzero if it hasn’t. As an alternative to waiting on the mutex before splitting its stack, a thread can call pthread_mutex_trylock. If it acquires term mutex, it can proceed as before. If not, it can just return. Presumably on a subsequent call it can successfully acquire the mutex.

Splitting the stack

Since our goal is to balance the load among the threads, we would like to insure that the amount of work in the new stack is roughly the same as the amount remaining in the original stack. We have no way of knowing in advance of searching the subtree rooted at a partial tour how much work is actually associated with the partial tour, so we’ll never be able to guarantee an equal division of work. However, we can use the same strategy that we used in our original assignment of subtrees to threads: that the subtrees rooted at two partial tours with the same number of cities have identical structures. Since on average two partial tours with the same number of cities are equally likely to lead to a “good” tour (and hence more work), we can try splitting the stack by assigning the tours on the stack on the basis of their numbers of edges. The tour with the least number of edges remains on the original stack, the tour with the next to the least number of edges goes to the new stack, the tour with the next number of edges remains on the original, and so on.

This is fairly simple to implement, since the tours on the stack have an increasing number of edges. That is, as we proceed from the bottom of the stack to the top of the stack, the number of edges in the tours increases. This is because when we push a new partial tour with k edges onto the stack, the tour that’s immediately “beneath” it on the stack either has k edges or k 1 edges. We can implement the split by starting at the bottom of the stack, and alternately leaving partial tours on the old stack and pushing partial tours onto the new stack, so tour 0 will stay on the old stack, tour 1 will go to the new stack, tour 2 will stay on the old stack, and so on. If the stack is implemented as an array of tours, this scheme will require that the old stack be “compressed” so that the gaps left by removing alternate tours are eliminated. If the stack is implemented as a linked list of tours, compression won’t be necessary.

This scheme can be further refined by observing that partial tours with lots of cities won’t provide much work, since the subtrees that are rooted at these trees are very small. We could add a “cutoff size” and not reassign a tour unless its number of cities was less than the cutoff. In a shared-memory setting with an array-based stack, reassigning a tour when a stack is split won’t increase the cost of the split, since the tour (which is a pointer) will either have to be copied to the new stack or a new

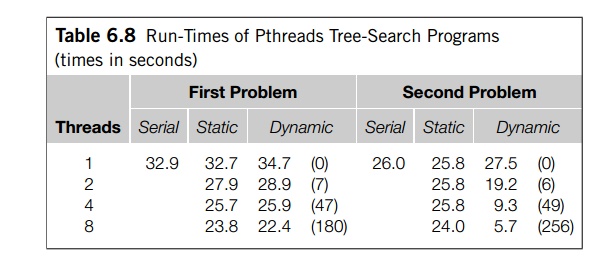
location in the old stack. We’ll defer exploration of this alternative to Programming Assignment 6.6.