Parallelizing the reduced solver using OpenMP

Parallelizing the reduced solver using OpenMP

The reduced solver has an additional inner loop: the initialization of the forces array to 0. If we try to use the same parallelization for the reduced solver, we should also parallelize this loop with a for directive. What happens if we try this? That is, what happens if we try to parallelize the reduced solver with the following pseudocode?

        # pragma omp parallel

        for each timestep {

if (timestep output) {

        # pragma omp single

Print positions and velocities of particles;

}

        # pragma omp for

for each particle q forces[q] = 0.0;

        # pragma omp for

for each particle q

Compute total force on q;

        # pragma omp for

for each particle q

Compute position and velocity of q;

}

Parallelization of the initialization of the forces should be fine, as there’s no depen-dence among the iterations. The updating of the positions and velocities is the same in both the basic and reduced solvers, so if the computation of the forces is OK, then this should also be OK.

How does parallelization affect the correctness of the loop for computing the forces? Recall that in the reduced version, this loop has the following form:

As before, the variables of interest are pos, masses, and forces, since the values in the remaining variables are only used in a single iteration, and hence, can be private. Also, as before, elements of the pos and masses arrays are only read, not updated. We therefore need to look at the elements of the forces array. In this version, unlike the basic version, a thread may update elements of the forces array other than those corresponding to its assigned particles. For example, suppose we have two threads and four particles and we’re using a block partition of the particles. Then the total force on particle 3 is given by

F₃ =   f₀₃ - f₁₃ - f₂₃.

Furthermore, thread 0 will compute f₀₃ and f₁₃, while thread 1 will compute f₂₃. Thus, the updates to forces[3] do create a race condition. In general, then, the updates to the elements of the forces array introduce race conditions into the code.

A seemingly obvious solution to this problem is to use a critical directive to limit access to the elements of the forces array. There are at least a couple of ways to do this. The simplest is to put a critical directive before all the updates to forces

However, with this approach access to the elements of the forces array will be effectively serialized. Only one element of forces can be updated at a time, and contention for access to the critical section is actually likely to seriously degrade the performance of the program. See Exercise 6.3.

An alternative would be to have one critical section for each particle. However, as we’ve seen, OpenMP doesn’t readily support varying numbers of critical sections, so we would need to use one lock for each particle instead and our updates would This assumes that the master thread will create a shared array of locks, one for each particle, and when we update an element of the forces array, we first set the lock corresponding to that particle. Although this approach performs much bet-ter than the single critical section, it still isn’t competitive with the serial code. See Exercise 6.4.

Another possible solution is to carry out the computation of the forces in two phases. In the first phase, each thread carries out exactly the same calculations it carried out in the erroneous parallelization. However, now the calculations are stored in its own array of forces. Then, in the second phase, the thread that has been assigned particle q will add the contributions that have been computed by the different threads. In our example above, thread 0 would compute -f₀₃ -f₁₃, while thread 1 would compute -f₂₃. After each thread was done computing its contributions to the forces, thread 1, which has been assigned particle 3, would find the total force on particle 3 by adding these two values.

Let’s look at a slightly larger example. Suppose we have three threads and six particles. If we’re using a block partition of the particles, then the computations in the first phase are shown in Table 6.1. The last three columns of the table show each thread’s contribution to the computation of the total forces. In phase 2 of the computation, the thread specified in the first column of the table will add the contents of each of its assigned rows—that is, each of its assigned particles.

Note that there’s nothing special about using a block partition of the particles. Table 6.2 shows the same computations if we use a cyclic partition of the particles.

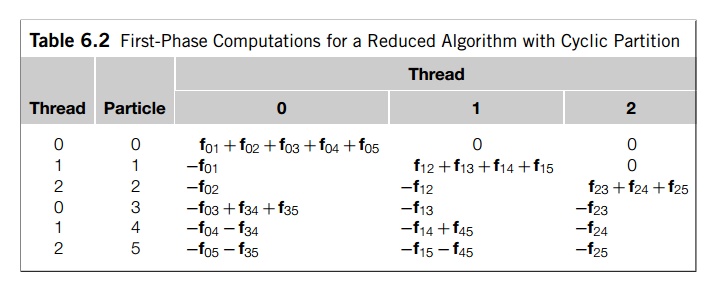
Note that if we compare this table with the table that shows the block partition, it’s clear that the cyclic partition does a better job of balancing the load.

To implement this, during the first phase our revised algorithm proceeds as before, except that each thread adds the forces it computes into its own subarray of loc_forces:

During the second phase, each thread adds the forces computed by all the threads for its assigned particles:

Before moving on, we should make sure that we haven’t inadvertently introduced any new race conditions. During the first phase, since each thread writes to its own subarray, there isn’t a race condition in the updates to loc_forces. Also, during the second phase, only the “owner” of thread q writes to forces[q], so there are no race conditions in the second phase. Finally, since there is an implied barrier after each of the parallelized for loops, we don’t need to worry that some thread is going to race ahead and make use of a variable that hasn’t been properly initialized, or that some slow thread is going to make use of a variable that has had its value changed by another thread.