Orthogonal Coordinate Systems

Other Orthogonal Coordinate Systems

The laws of tensor transformation [Equation (2.13) or Mohr's Circle] allow us to describe stress or strain in any orientation of coordinate axes once we have solved for the tensor in one particular orthogonal set. In many physical situ-ations, the field equations, which have been derived in a global, rectangular coordinate system, can be more easily solved in some other coordinate system.

Rather than re-derive them from consideration of stress and geometry changes for a new differential element in each coordinate system, it is easier to present the most general form and show how it can be reduced in each specific case.** The differential equations of equilibrium relative to general

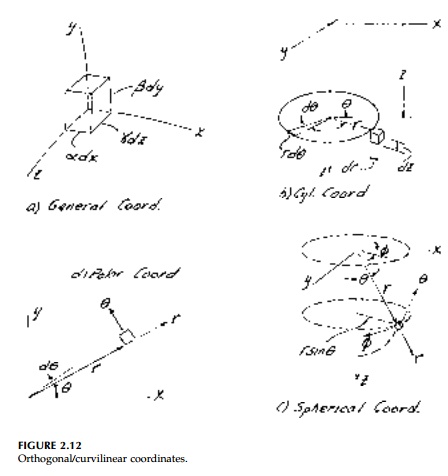
in which (?, ?, ?) are metric coefficients which are functions of the coordi-nates (x, y, z) defined by

where ds is the differential diagonal of the element (Figure 2.12a) with edge 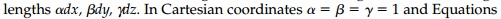  lengths ?dx, ?dy, ?dz. In Cartesian coordinates ?= ?=?=1 and Equations (2.45) reduce to Equation (2.43).

The strain-displacement equations for the element are:

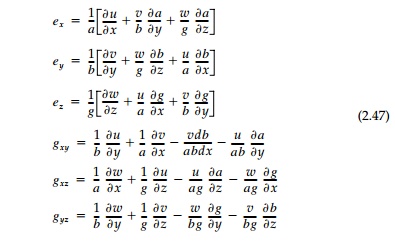
where u,v,w are the projections of the displacement vector of point x,y,z on the tangents to the coordinate lines at the point.

Cylindrical Coordinates (r, , z)

Let x = r, y=  , z = z as shown in Figure 2.12b. Then:

Spherical Coordinates (r, , )

Let x = r, y = , z =  where   is the latitude and  the longitude as shown in Figure 2.12c. The equilibrium equations become:

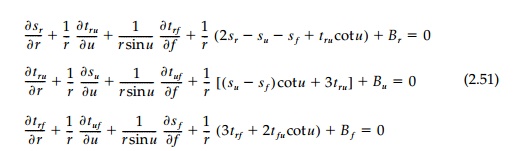
The strain-displacement relations in spherical coordinates from Equation (2.47) become:

Plane Polar Coordinates (r, )

Polar coordinates for plane problems are, it will turn out, equally as useful as Car-tesian coordinates. They can be considered a special case of cylindrical coordi-nates where rz =z = (d/dz) = 0 and from Equation (2.49), equilibrium requires