Isotropic and Deviatoric Components

Isotropic and Deviatoric Components

As we have seen in previews Section , any symmetric tensor can be split into isotro-pic and deviatoric components as follows:

a)     For strain:

The isotropic component, E_m, ?_m is essentially a scalar (tensor of order zero) having only magnitude with all directions principal. It is sometimes called the spherical component. The mean stress, ?_m, is hydrostatic pressure if neg-ative, or suction if positive, and causes only volume change, 3E_m, per unit volume. The deviatoric component is just the opposite in that it causes only distortion or shear with no volume change. The invariants of the deviatoric tensors are:

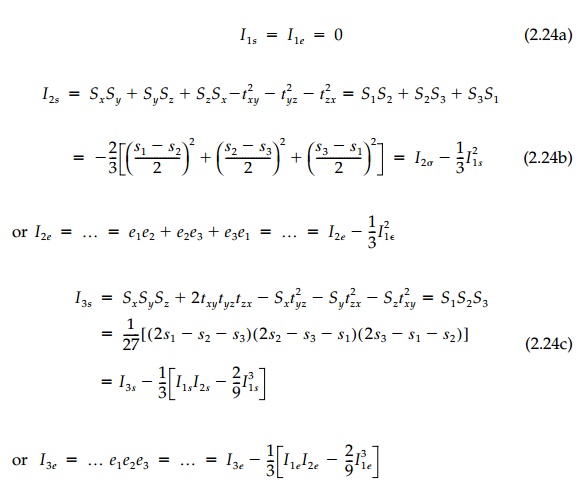
This uncoupling of the tensor into isotropic and deviatoric parts will turn out to be a fundamental physical reality that is reflected both in the way materials behave under load, and how the stress, strain, and displacements 'flow' through a body. It also turns out that there is a particular orientation of axes (of viewing the tensor) where, in fact, this fundamental uncoupling occurs naturally and the tensor components become the invariants them-selves. This is the so-called octahedral state.