Principal Space and the Octahedral Representation

Principal Space and the Octahedral Representation

Since the principal stresses are orthogonal, we can, once we calculate their directions by the procedure in Section, imagine that now the x, y, z, axes of Figure 2.4 are oriented in the principal directions. Thus plane ABC, as redrawn in Figure 2.5a, is normal to a straight line x' from the origin with

direction cosines with respect to the 1, 2, 3 axes. For convenience let the z' axis lie in the 1-3 plane. From Equation (2.12) then:

Of particular interest is the special case in Figure 2.5a where l, m, n all equal 1/ 3^1/3 . This direction is the diagonal of a unit cube and thus often called the 'space diagonal.' For this orientation:

The subscript designation 'oct' or o is used since there are eight such faces normal to the space diagonals forming a regular octahedron as in Figue 2.5d. The total 'stress resultant' on an octahedral plane is:

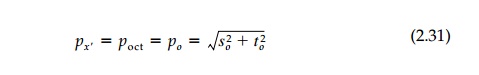
As already mentioned, the remarkable property of this octahedral orien-tation is, as shown by Equation (2.28), that the stress or strain tensors uncouple naturally* into invariant isotropic and deviatoric components when viewed in this perspective in principal space. Moreover, the angle in Equation (2.30) is related to I_?3 or more specifically to I_s3 / ( Is2)2/3 so that all three invariants appear on the octahedral plane. Thus, in this one special orientation, the tensor can be reduced (visualized) in its most physical form as three numbers (scalar invariants) ?_oct, ?_oct, ? and three direction cosines relating the direction of the space diagonal (the octahedral plane) to the coordinate system.**

The corresponding octahedral strain components are, by analogy:

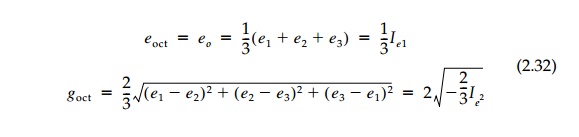
with components corresponding to Equations (2.29) and (2.30).