Chapter: Civil : Principles of Solid Mechanics : Strain and Stress
Deformation (Relative Displacement)
Deformation
(Relative Displacement)
Almost all displacement
fields induced by boundary loads, support movements, temperature, body forces,
or other perturbations to the initial condition are, unfortunately, nonlinear;
that is: u, v, and w are cross-products or power functions
of x, y, z (and perhaps other variables). However, as
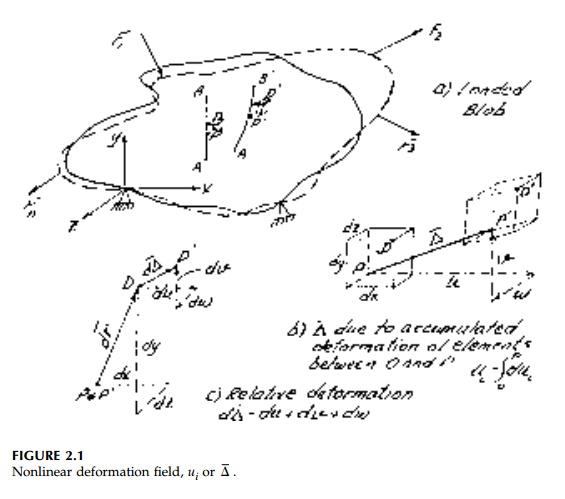
shown in Figure. 2.1,* the fundamental linear assumption of calculus allows us
to directly use the relations of finite linear transformation to depict immediately
the relative displacement or deformation du, dv, dw of a
differential element dx, dy, dz.
On a differential scale, as long as u,
v, and w are continuous, smooth, and small, straight lines remain
straight and parallel lines and planes remain par-allel. Thus the standard
definition of a total derivative:
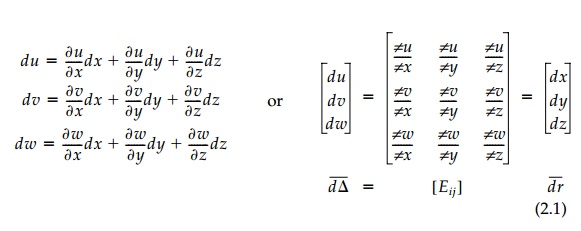
is more than a mathematical statement
that differential base lengths obey the laws of linear transformation.** The
resulting deformation tensor, Eij, also
called the relative displacement tensor,
is directly analogous to the linear displacement tensor, ?ij,
of coming pages, which transformed finite base-lengths. The elements of Eij
(the partial derivatives), although nonlinear functions throughout the field
(i.e., the structure), are just numbers when evaluated at any x, y,
z. Therefore Eij should be thought of as an average
or, in the limit, as 'deformation at a point.' Displacements u, v,
w, due to defor-mation, are obtained by a line integral of the total
derivative from a location where u, v, w have known
values; usually a support where one or more are zero. Thus:
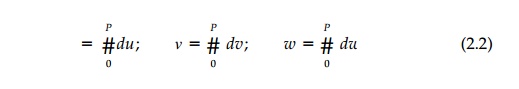
Related Topics