Two Dimensional Stress or Strain

Two Dimensional Stress or Strain

In the majority of important practical situations, the general three-dimensional stress-strain array (Figure 2.3e) can, to an acceptable degree of accuracy, be simplified to a 4-component symmetric tensor by assuming either no stress or no strain components on one set of planes (say the z faces). The first is called 'plane stress' corresponding to free surfaces normal to the z axis so that ?_z =?_xx =?_zy =0 and is the most common and the most easily achieved in the laboratory. For plane stress there will generally be strain normal to the unrestrained z planes (e_z Not equal to 0) but no shearing distortion (i.e., ?_zy = ?_zx = 0).

'Plane strain' arises physically in situations such as dams, pipelines, embankments, long shafts, etc. where there are no displacements in the z direction nor distortion in the z plane. Therefore E_z =? _zx = ?_zy = 0. In general for plane strain ?_z!= 0 but ?_zx =?_zy = 0.

Thus, in either case, the in-plane tensor reduces to:

?_z and E_Z are principal and either I₃? or I₃? is zero.*

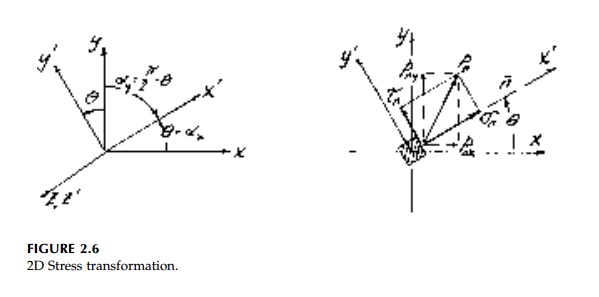
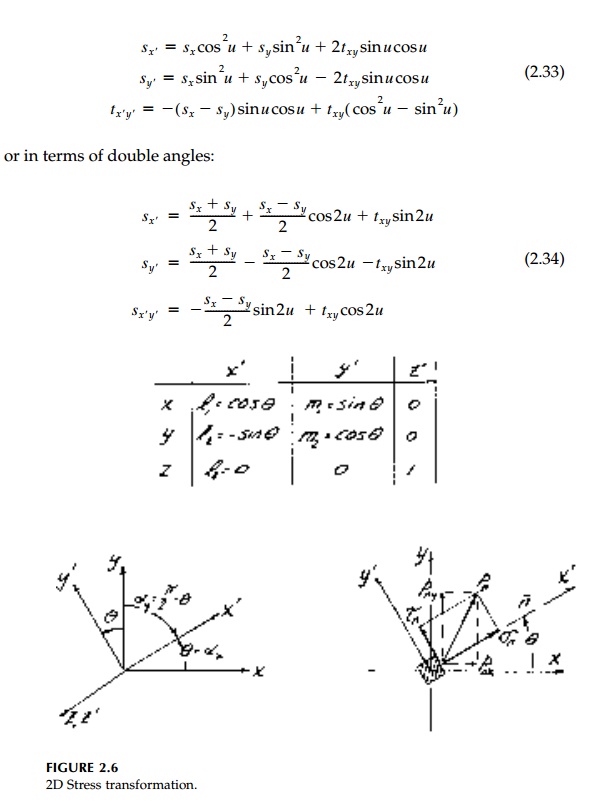
The 2D transformation (rotation of coordinate axes) from the z, y, z to a new x, y, z axes can be deduced from the 3D equations [Equations (2.13)]. The direction cosines in terms of the positive counterclockwise angle of axis rota-tion  are shown in Figure 2.6.

Therefore,

The transformation of the 2D strain tensor is the same by analogy, with E_x, E_y , ?_xy/2, replacing ?_x?_y?_xy .

The 2D characteristic equation becomes

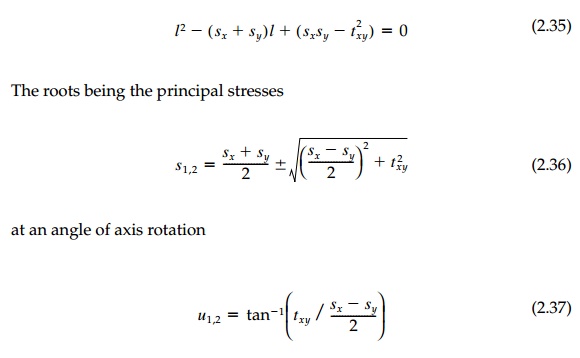
The coefficients of the characteristic equation must again be the same in any orientation so the 2D invariants are:

In principal space the 'octahedral' orientation along the 'space diagonal' becomes the 'quadrahedral' orientation along the 'square diagonal.' In this orientation the quadrahedral stress components are:

Thus in the quadrahedral orientation, we again see all the invariants as indi-vidual, uncoupled stress components in themselves. There can be no doubt that this is what nature actually feels at a point in a 2D stress field. Again the analogous equations for the 2D strain tensor in the plane [Equations (2.35)-(2.42)] are obtained by substituting E_x for ?_x, E_y, for ?_y, ?_xy /2 for ?_xy.

Perhaps it should be noted that the elastic rotation around the z axis in two dimensions _xy ?2 or ?_z of Equation (2.5) (the asymmetric component of the relative deformation tensor) is already an invariant.* While in 3D the elastic rotation is a vector with three components, in 2D, ?_z =? _q at a point is actually a scalar quantity involving only magnitude since the direction is known. There is no comparable asymmetric component of stress, but elastic rotations occur due to stress fields and must not be forgotten while we are preoccupied with symmetric stress and strain tensors.